Práctica 0. Introducción.
Una de las maneras de seguir las prácticas en Matlab consiste en ejecutarlas como una demo. En esta introducción mostramos los pasos para ejecutar una demo y veremos algunos ejemplos.
Contents
Uso de una demo
Una demo contiene textos y grupos de instrucciones que se van ejecutando paso a paso en la ventana de 'Comandos' (Command Window). Por ejemplo la siguiente instrucción calcula el valor de la función seno tomando como argumento 3*pi/2 radianes. Puede observar la instrucción y el resultado.
sin(3*pi/2)
ans =
-1
Tras cada grupo de instrucciones se produce una pausa, y aparece (en la parte superior de la ventana de 'Comandos') la opción de continuar con el siguiente grupo de instrucciones 'Next', de finalizar la demo 'Stop' o de abrir en el editor la demo pinchando en el nombre de la demo. Si quisiera ver un grupo de instrucciones ejecutadas con anterioridad, podría desplazar hacia arriba la ventana de 'Comandos', o parar la demo y volver a ejecutarla desde el principio. -> Pulse ahora 'Next' para ejecutar el siguiente grupo de instrucciones.
Ejecutar una demo
Para ejecutar una demo se puede introducir el comando 'echodemo nombredelademo.m' suponiendo que tenga el archivo descargado en el 'directorio actual' (Current Directory). Puede cambiar el directorio actual pinchando con el ratón a la derecha de la barra de 'directorio actual'.
A partir de ahora no se le pedirá que pulse en 'Next' para ejecutar el siguiente grupo de instrucciones.
Al acabar cada grupo de instrucciones aparece en la ventana de 'Comandos' el símbolo >> que indica que puede introducir comandos antes de seguir (reproduciendo) la demo.
Tras algunos grupos de instrucciones aparecerán ejercicios que debe realizar, tecleando las instrucciones necesarias, antes de continuar con la demo.
Ej 1. Teclee en la ventana 'Command Window' la instrucción 2+2 y pulse la tecla Enter. Compruebe que ha obtenido el resultado 4 antes de continuar con el siguiente grupo de instrucciones de esta demo. (Recuerde dónde debe pulsar al acabar el ejercicio para ejecutar las siguientes instrucciones de la demo)
Uso de la ayuda
En cualquier momento puede pulsar la tecla F1 para abrir la ventana de ayuda, o pedir ayuda en la ventana de comandos con la instrucción help, como por ejemplo.
help echodemo
ECHODEMO Run a cell script as an echo-and-pause command line demo.
ECHODEMO FILENAME displays a cell script FILENAME. Cell scripts can be
created using Cell Mode in the MATLAB Editor. The demo is advanced by
clicking on HTML hypertext links embedded in the command window.
ECHODEMO('FILENAME',CELLINDEX) evaluates the cell number given by
CELLINDEX.
doc echodemo
Observe que se le ha mostrado, en inglés, ayuda sobre el comando echodemo, y que aunque en la ayuda los comandos aparezcan en mayúscula como 'ECHODEMO', debe teclearlos en minúsculas.
Otra forma de obtener ayuda consiste, como le ha indicado la ayuda que acabamos de ver, en ejecutar el comando doc.
Ej 2. Introduzca el comando 'doc echodemo' y cierre la ventana de ayuda para seguir con esta demo.
Orden de las operaciones
Al evaluar una expresión, Matlab efectúa las potencias antes que los productos y divisiones. Y los productos y las divisiones las efectúa antes que las sumas y las restas. Observe como las siguientes parejas de instrucciones dan resultados distintos.
1+1/2 (1+1)/2
ans =
1.5000
ans =
1
2^3+1 2^(3+1)
ans =
9
ans =
16
Acumulador (suma)
Ahora vamos a implementar un algoritmo sencillo en el que usamos un acumulador para calcular la suma de N números. (Estas instrucciones se encuentran en el archivo acumulador_suma.m )
% Definimos un vector que contiene los números que vamos a sumar x=[2 4 9 3 6 0 3 2 1 8 6 7 5] % Hallamos el número de elementos del vector N=length(x) % Inicializamos el acumulador s=0; % Sumamos al acumulador cada uno de los elementos del vector x for i=1:N s=s+x(i); end % Mostramos el resultado disp('La suma de las componentes es:') disp(s)
x =
Columns 1 through 11
2 4 9 3 6 0 3 2 1 8 6
Columns 12 through 13
7 5
N =
13
La suma de las componentes es:
56
Vectorización (suma)
En este caso se puede hallar la suma de las componentes del vector x de una forma más eficiente sin emplear un bucle for, usando la función sum.
sum(x)
ans =
56
Ej 3. Defina un vector llamado y que contenga las cifras de su DNI o pasaporte. Use un acumulador para hallar la suma de las componentes del vector y. Obtenga el mismo resultado usando la función sum.
Gráficas.
Una gráfica en Matlab puede representarse de forma sencilla usando el comando plot.
Con la instrucción plot(x,y) podemos unir un grupo de puntos para formar una gráfica. El vector x contiene las coordenadas horizontales (abscisas) de los puntos. El vector y contiene las coordenadas verticales (ordenadas).
Como ejemplo definimos un vector x con los valores 0, 0.5, 1, 1.5, ..., 8, 8.5 y 9. También definimos un vector y con los cuadrados de los elementos de x.
x=[0:0.5:9] y=x.^2 plot(x,y)
x =
Columns 1 through 6
0 0.5000 1.0000 1.5000 2.0000 2.5000
Columns 7 through 12
3.0000 3.5000 4.0000 4.5000 5.0000 5.5000
Columns 13 through 18
6.0000 6.5000 7.0000 7.5000 8.0000 8.5000
Column 19
9.0000
y =
Columns 1 through 6
0 0.2500 1.0000 2.2500 4.0000 6.2500
Columns 7 through 12
9.0000 12.2500 16.0000 20.2500 25.0000 30.2500
Columns 13 through 18
36.0000 42.2500 49.0000 56.2500 64.0000 72.2500
Column 19
81.0000
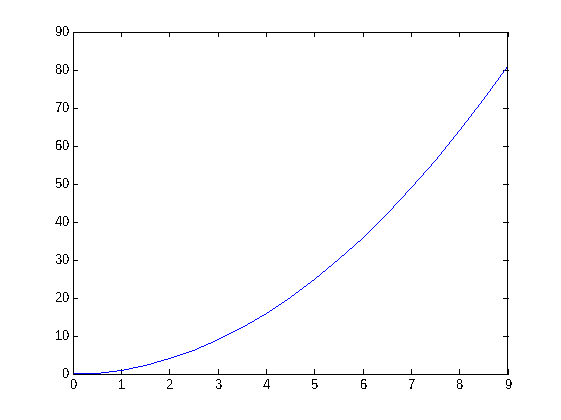
Observe que al definir el vector y estamos aplicando la operación 'elevar al cuadrado' a todas las componentes del vector x, por eso ponemos un punto antes del símbolo de potencia.
Para representar simultáneamente dos gráficas podemos emplear la instrucción plot(x1,y1,x2,y2) donde los vectores x1 e y1 contienen las coordenadas de una gráfica, y los vectores x2 e y2 contienen las coordenadas de otra gráfica.
En el siguiente ejemplo representamos conjuntamente las rectas y=x+1 e y=2x-1.
plot(x, x+1, x, 2*x-1)
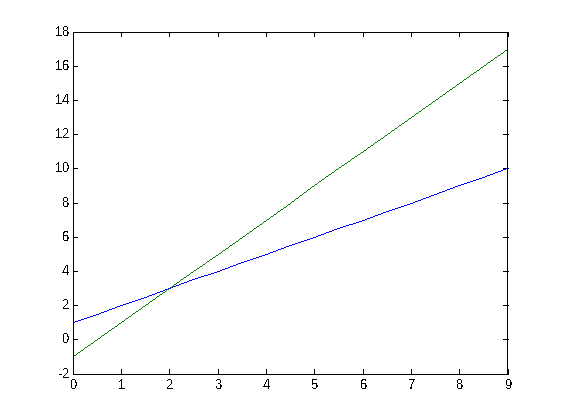
Ejercicios finales.
Al final de cada práctica le aparecerán algunos ejercicios que deberá realizar. Si escribe los ejercicios en un script podrá usarlos más tarde, modificarlos o repasarlos. Al grabar el script use la extensión .m y no incluya en el nombre del script ni acentos ni espacios. Se recomienda poner comentarios (con el símbolo de tanto por ciento) en los archivos script, para facilitar su modificación o repaso.
Ej 4. Represente conjuntamente la gráfica del seno y del polinomio p(x)=x-x^3/6+x^5/120 en el intervalo [-3.15,3.15]. Puede obtener la gráfica escribiendo las siguientes cuatro instrucciones.
- Defina un vector x formado por los elementos -3.15, -3.14, -3.13, ..., -0.01, 0, 0.01, 0.02, ..., 3.14, 3.15.
- Obtenga un vector f con el seno de cada uno de los valores del vector x.
- Obtenga un vector g aplicando el polinomio p(x)=x-x^3/6+x^5/120 a los elementos del vector x.
- Represente conjuntamente las gráficas de la función seno y del polinomio p(x) empleando los vectores f y g.
Puede ahora observar como el polinomio aproxima a la función seno en valores más lejanos al cero representando ambas funciones en el intervalo [-7.15, 7.15].
Ej 5. Represente conjuntamente la gráfica del coseno y del polinomio q(x)=1-x^2/2+x^4/24 en el intervalo [-3.15,3.15].
Ej 6. Obtenga a=sen(0.3) y b=p(0.3), donde p es el polinomio definido en el ejercicio 4. Halle a-b. (Solución : a=0.2955, b=0.2955, a-b=-4.3339e-008)
Observe que si se muestran a y b con cinco cifras decimales (representación por defecto al usar 'format short') ambos valores tienen la misma representación. Al hallar la resta o emplear una representación con más decimales (como con 'format long') se puede apreciar la diferencia entre los dos valores.
Ej 7. Obtenga a=cos(0.4) y b=q(0.4), donde q es el polinomio definido en el ejercicio 5. Halle a-b. (Solución : a=0.9211, b=0.9211, a-b= -5.6727e-006).
Al acabar la clase se recomienda que almacene o se envíe los script que haya creado. A continuación puede reiniciar el ordenador, o apagarlo, dependiendo de si hay un turno de prácticas después del suyo, o no.
% Ecuaciones Diferenciales y Cálculo Numérico. (A. Palomares) % Grado en Ingeniería de Tecnologías de Telecomunicación. disp(date)
22-Feb-2024