Práctica 2. Ecuaciones en Derivadas Parciales.

Veremos cómo implementar métodos numéricos basados en diferencias finitas para resolver aproximadamente la ecuación de ondas, la ecuación del calor y la ecuación de Poisson.

Método explícito para el problema mixto para la ecuación de ondas
Condiciones iniciales para la ecuación de ondas.
Primeros valores de U.
Bucle general para la ecuación de ondas.
Resultados para la ecuación de ondas.
Método explícito para el problema mixto para la ecuación del calor
Inicialización para la ecuación del calor.
Resultados de la ecuación del calor.
Método para la ecuación de Poisson.
Inicialización.
Variables correspondientes a los puntos del borde.
Esquema de diferencias finitas.

Método explícito para el problema mixto para la ecuación de ondas

En esta sección vamos a implementar en Matlab/Octave el método explicado en teoría. Debemos tener en cuenta que aunque matemáticamente se pueda definir un subíndice de una variable como cero, los elementos de las matrices (y los índices en Matlab/Octave) empiezan en 1.

Como ejemplo, nos planteamos el problema

(parcial segunda de u respecto de t dos veces) - 4*(parcial segunda de u respecto de x dos veces) = 0 para t>=0, x en [0,6],

u(0,x)=x*(x-6)^2,

parcial de u respecto de t en (0,x)=0, para x en [0,6],

u(t,0)=u(t,2)=0, para t>=0. donde discretizamos en el dominio [0,2] x [0,6] de forma que en el dominio del tiempo haya 2 subintervalos y en el dominio de x haya 3 subintervalos.

% Comenzamos definiendo la función phi que define la deformación inicial de la cuerda.
% La definimos de forma que se pueda usar en vectores.
phi=@(x) x.*(x-6).^2;

La solución del problema será una función u(t,x) donde la variable t está en el intervalo [0,T] dividido en N intervalos y la variable x está en el intervalo [0,ele] dividido en M intervalos.

T=2;
ele=6;
N=2;
M=3;

Como el intervalo [0,T] está dividido en N subintervalos, cada uno de estos subintervalos tendrá longitud Deltat=T/N. De la misma manera, como el intervalo [0,ele] está dividido en M subintervalos, cada uno tendrá longitud Deltax=ele/M. Con esto podemos definir los puntos que utilizamos para dividir los intervalos (y que dan la 'red uniforme' de la que se habla en la teoría).

Deltat=T/N;
Deltax=ele/M;
nodost=[0:Deltat:T];
nodosx=[0:Deltax:ele];

Definimos el coeficiente c a partir de la ecuación en derivadas parciales y el valor de q que se usará en las ecuaciones de diferencias finitas.

c=2; % c^2 es el coeficiente de la parcial segunda de u respecto de x dos veces.
q=c*Deltat/Deltax;

Inicializamos una matriz en la que almacenaremos las aproximaciones de u en los puntos de la red uniforme.

U=zeros(N+1,M+1);

Condiciones iniciales para la ecuación de ondas.

Definimos la deformación inicial de la cuerda. U(1,j)=phi( Deltax*(j-1) ) . Ahorramos un bucle aplicando phi a los nodos en el eje x.

U(1,:)=phi(nodosx);
% Ahora imponemos que la cuerda está sujeta en el extremo izquierdo x=0,
% que es equivalente a definir en un bucle U[i,1]=0 para i=1,2,...,N+1 .
U(:,1)=0;
% También la cuerda está sujeta en el extremo derecho x=ele ,
% que es equivalente a definir en un bucle U[i,M+1]=0 para i=1,2,...,N+1 .
U(:,M+1)=0;

Primeros valores de U.

Aquí usamos diferencias finitas para calcular U en el siguiente instante tras la deformación inicial de la cuerda. En la teoría estos valores se notaban con subíndices U1,j con i=1, pero aquí usamos la notación U(2,j). No llegamos hasta U(2,M+1) porque ya sabemos que vale cero.

for j=2:M
    U(2,j)=(1-q^2)*U(1,j)+(q^2/2)*( U(1,j+1)+U(1,j-1) );
end

Bucle general para la ecuación de ondas.

Ahora usamos el esquema de diferencias finitas visto en teoría para el resto de puntos de la red uniforme. Empezamos calculando U(3,j), porque el U(2,j) ya se calculó en el anterior bucle.

for i=2:N
 for j=2:M
 U(i+1,j)=2*(1-q^2)*U(i,j)+q^2*( U(i,j+1)+U(i,j-1) )-U(i-1,j) ;
 end
end

Resultados para la ecuación de ondas.

La matriz U contiene los valores aproximados de la función u.

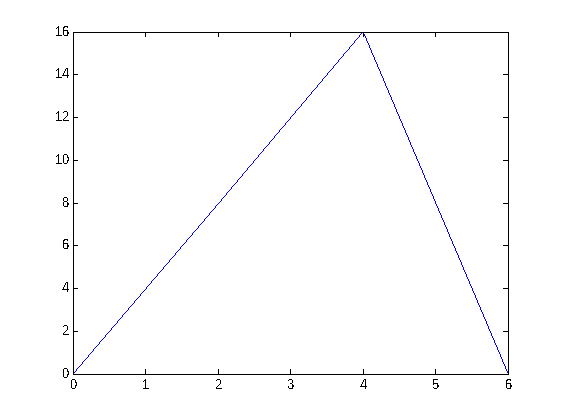
U
plot(nodosx, U(1,:) ) % Gráfica de la posición inicial i=1, t=0 .
disp('Pulse una tecla para ver la siguiente gráfica');
pause
plot(nodosx, U(2,:) )  %Gráfica del momento i=2, t=Deltax .
% Representar U.
% stem3(nodost,nodosx,U')

U =

     0    32    16     0
     0     8    16     0
     0   -16    -8     0

Pulse una tecla para ver la siguiente gráfica

Ej. Se quiere hallar una aproximación a la solución del siguiente problema mixto para la ecuación de ondas

(parcial segunda de u respecto de t dos veces) - (parcial segunda de u respecto de x dos veces) = 0 para t>=0, x en [0,2],

u(0,x)=sen(pi*x/2),

parcial de u respecto de t en (0,x)=0, para x en [0,2],

u(t,0)=u(t,2)=0, para t>=0.

Aplique el método explícito en diferencias finitas, dividiendo el dominio [0, 6] x [0, 2] en intervalos de longitud 2 en la variable t e intervalos de longitud 1 en el dominio de la variable x . (Sol. U=[ 0 1 0 ; 0 -3 0; 0 17 0; 0 -99 0 ] )

Método explícito para el problema mixto para la ecuación del calor

Es este apartado nos planteamos hallar la solución aproximada de la ecuación del calor. Usaremos la misma notación y la misma discretización del dominio que en la ecuación anterior. El cambio en la ecuación en derivadas parciales afectará a las ecuaciones en diferencias finitas.

Nos planteamos el problema (parcial de u respecto a t) - (parcial segunda de u respecto a x dos veces) = 0, para t>=0, x en [0,3],

u(0,x)=sen(pi*x/3), para x en [0,3],

u(t,0)=u(t,3)=0, t>=0, donde consideramos el dominio del tiempo [0,9] dividido en 3 subintervalos y el dominio [0,3] para la variable x, dividido en 3 intervalos.

Inicialización para la ecuación del calor.

Comenzamos definiendo la función phi que es la temperatura inicial de la barra, y discretizamos en los ejes del tiempo y del espacio.

phi=@(x) sin(pi*x/3);
T=9;
ele=3;
N=3;
M=3;
Deltat=T/N;
Deltax=ele/M;
nodost=[0:Deltat:T];
nodosx=[0:Deltax:ele];

Definimos el coeficiente de la ecuación en derivadas parciales y una matriz que contendrá las aproximaciones a los valores de u.

c=1; % Coeficiente de la parcial segunda de u respecto de x dos veces.
q=c*Deltat/(Deltax^2);
U=zeros(N+1,M+1);

Imponemos las condiciones de contorno.

U(1,:)=phi(nodosx);
U(:,1)=0;  %U(i,1)=0 para i=1,2,...,N+1 .
U(:,M+1)=0;  %U(i,M+1)=0 para i=1,2,...,N+1 .

Ahora escribimos el bucle general usando el esquema en diferencias finitas. En este caso tenemos que empezar por i=1, para calcular U(2,j). Esto cambia con respecto al caso anterior.

for i=1:N
 for j=2:M
 U(i+1,j)=(1-2*q)*U(i,j)+q*( U(i,j+1)+U(i,j-1) ) ;
 end
end

Resultados de la ecuación del calor.

Para comprobar los resultados recordamos que -sqrt(3) = -1.7321, 2*sqrt(3) = 3.4641, -4*sqrt(3)= -6.9282 .

U =

         0    0.8660    0.8660         0
         0   -1.7321   -1.7321         0
         0    3.4641    3.4641         0
         0   -6.9282   -6.9282         0

Ej. Considere el siguiente problema mixto para la ecuación del calor (parcial de u respecto a t) - 2*(parcial segunda de u respecto a x dos veces) = 0, para t>=0, x en [0,4],

u(0,x)=x*(4-x), para x en [0,4],

u(t,0)=u(t,4)=0, t>=0.

Halle una aproximación a la solución usando el método explícito en diferencias finitas en el dominio [0,4] x [0,4], dividiendo en intervalos de longitud 2 en el eje de variable t y en intervalos de longitud 1 en el eje de la variable x . (Sol. U=[ 0 3 4 3 0 ; 0 -5 -4 -5 0 ; 0 19 -12 19 0 ] )

Método para la ecuación de Poisson.

En esta sección nos planteamos la ecuación de Poisson (laplaciano de u igual a una función dada f). Al implementar este método, tendremos que resolver un sistema de ecuaciones lineales para obtener las aproximaciones de la función U. Al plantear el sistema lineal, el vector término independiente contiene valores de f(xi,yj) y el vector de soluciones contiene valores de u. Será necesario reordenar los elementos de una matriz para que tengan forma de vector.

Nos planteamos el problema de aproximar una función u(x,y) definida en un dominio D=[0,3]x[0,3] de forma que

su laplaciano cumple (parcial segunda de u respecto a x dos veces) + (parcial segunda de u respecto a y dos veces) = 6(x+y), para (x,y) en D.

u(x,y)= x^3+y^3, para (x,y) en la frontera de D. Para el método consideramos el dominio de la x dividido en tres subintervalos y el dominio de la y dividido en tres subintervalos.

Inicialización.

Extremos del intervalo para el eje x y subintervalos.

a=0;
b=3;
N=3;
Deltax=(b-a)/N;
nodosx=[a:Deltax:b];

Extremos del intervalo para el eje y y subintervalos.

c=0;
d=3;
M=3;
Deltay=(d-c)/M;
nodosy=[c:Deltay:d];

% Definición de la función en la frontera.
phi=@(x,y)  x^3+y^3;

% Definición de la función f igual al laplaciano.
f=@(x,y) 6*(x+y);

% Inicializamos U
U=zeros(N+1,M+1);

% Inicializamos A y B para el sistema de ecuaciones.
A=zeros( (N+1)*(M+1), (N+1)*(M+1) );
B=zeros( (N+1)*(M+1), 1 );

La función q transforma los valores i=1,..,N+1, j=1,...,M+1 en valores de q=1,...,(N+1)*(M+1).

q=@(i,j) (j-1)*(N+1)+i;

Variables correspondientes a los puntos del borde.

Usamos la función phi de las condiciones de contorno para definir las ecuaciones correspondientes a los valores de u en el borde.

for j=1:M+1
    % U(1,j)=phi(a, nodosy(j) );
    A( q(1,j),q(1,j) )=1;
    B( q(1,j) )=phi(a, nodosy(j) );

    % U(N+1,j)=phi(b, nodosy(j) );
    A( q(N+1,j),q(N+1,j) )=1;
    B( q(N+1,j) )=phi(b, nodosy(j) );
end

for i=1:N+1
    %U(i,1)=phi( nodosx(i), c);
    A( q(i,1),q(i,1) )=1;
    B( q(i,1) )=phi( nodosx(i), c);

    %U(i,M+1)=phi( nodosx(i), d);
    A( q(i,M+1),q(i,M+1) )=1;
    B( q(i,M+1) )=phi( nodosx(i), d);
end

Esquema de diferencias finitas.

Montamos el sistema de ecuaciones que nos permite hallar los valores de U. Estas ecuaciones se deducen al aplicar diferencias finitas a los puntos interiores del dominio.

Queremos escribir la siguiente ecuación en forma matricial (1/Deltax^2)*U(i+1,j) - (2/Deltax^2)*U(i,j) + (1/Deltax^2)*U(i-1,j) + + (1/Deltay^2)*U(i,j+1)-(2/Deltay^2)*U(i,j)+(1/Deltay^2)*U(i,j-1) = f( nodosx( i ), nodosy( j ) ) Cada valor de (i,j) nos da una ecuación distinta, que numeramos como ec=q(i,j) con término independiente f( nodosx( i ), nodosy( j ) ) y con coeficicientes (1/Deltax^2), ... que introducimos en la matriz A.

for i=2:N
    for j=2:M
    % Estamos en la ecuación con término independiente
    % f( nodosx( i ), nodosy( j ) )
    ec = q(i,j); %Número de la ecuación.
    %
    A( ec, q(i+1,j) ) = (1/Deltax^2);
    A( ec, q(i,j) )      = -(2/Deltax^2) -(2/Deltay^2);
    A( ec, q(i-1,j) )  =  (1/Deltax^2);
    %
    A( ec, q(i,j+1) ) = (1/Deltay^2);
    A( ec, q(i,j-1) )  = (1/Deltay^2);
    %
    B( ec ) = f( nodosx( i ), nodosy( j ) );
    end
end

Resolvemos el sistema con la 'división izquierda'.

X=A\B

El vector X tiene (N+1)*(M+1) componentes que son aproximaciones de los valores de U en los nodos. Recuperamos la matriz U.

for i=1:N+1
    for j=1:M+1
        U(i,j)=X( q(i,j) );
    end
end

U

U =

         0    1.0000    8.0000   27.0000
    1.0000    2.0000    9.0000   28.0000
    8.0000    9.0000   16.0000   35.0000
   27.0000   28.0000   35.0000   54.0000

Ej. Aplique el método en diferencias finitas para hallar una aproximación a la solución del siguiente problema de contorno para la ecuación de Laplace en el dominio D formado por los puntos (x,y) que cumplen 0<x<4, 0<y<2 .

(parcial segunda de u respecto a x dos veces) + (parcial segunda de u respecto a y dos veces) = 0, para (x,y) en D.

u(x,y)=y^2-x^2, para (x,y) en la frontera de D.

Para el método, divida el dominio en ambas variables en subintervalos de longitud 1. Compare los valores aproximados obtenidos con los de la función u(x,y)=y^2-x^2. (Sol. U = [ 0 1 4 ; -1 0 3 ; -4 -3 0 ; -9 -8 -5 ; -16 -15 -12 ] = valores_exactos ).

% Ecuaciones Diferenciales y Cálculo Numérico. (A. Palomares)
% Grado en Ingeniería de Tecnologías de Telecomunicación.
disp(date)

20-Apr-2023