Práctica 6. Mínimos cuadrados
Contents
Ajuste lineal por mínimos cuadrados
Supongamos que tenemos un conjunto de puntos del plano (x1, y1), (x2, y2), ..., (xm, ym) y queremos hallar una recta de la forma y = a x + b que pase por esos puntos del plano o que 'pase lo más cerca posible' (en un sentido que se precisará).
Si los puntos estuvieran en una linea recta, podrían encontrarse valores a y b que serían una solución exacta del siguiente sistema lineal :
a x1 + b = y1, a x2 + b = y2, ... a xm + b = ym.
Este sistema se puede expresar de forma matricial. Si definimos
A=[ [ x1, 1 ];
[ x2, 1 ];
...
[ xm, 1 ] ]X=[ a ; b ]
B=[ y1 ;
y2 ;
...
ym ]entonces el sistema planteado se escribiría A*X = B.
En el caso en que los puntos no estén en una linea recta, no será posible encontrar valores de a y b que hagan que A*X sea igual a B, es decir el sistema A*X=B será incompatible.
En tal caso nos podemos plantear el problema de encontrar valores a y b que hagan que a*xi + b esté cerca de yi, en el sentido de que la suma de los valores (a*xi + b - yi)^2 sea la mínima posible. En la teoría esta suma se nota con la letra G y los valores yi provienen de valores f(xi) de una función real.
Este criterio para hallar a y b es equivalente a minimizar la distancia entre los vectores A*X y B en el sentido de la norma 2 y también es equivalente a encontrar la mejor aproximación por mínimos cuadrados discreta del vector (y1, y2, ..., ym) en el subespacio vectorial generado por los vectores (1, 1, ..., 1) y (x1, x2, ..., xm). Precisamente estos dos vectores constituyen las columnas de la matriz A.
Este problema, llamado de ajuste lineal por mínimos cuadrados, puede plantearse y resolverse de forma rigurosa usando el concepto de la mejor aproximación en un espacio normado. De este planteamiento puede deducirse que la solución X de este problema verifica un sistema lineal cuya matriz (de Gram) está formada por los productos escalares de los vectores (1, 1, ..., 1) y (x1, x2, ..., xm), y el término independiente del sistema son los productos escalares de los vectores (1, 1, ..., 1) y (x1, x2, ..., xm) por el vector (y1, y2, ..., ym) . Todos estos productos escalares, y el sistema lineal con la matriz de Gram se puede plantear en la siguiente ecuación matricial
transpose(A)*A*X = transpose(A)*B
que es un sistema compatible determinado siempre que dos valores xi sean distintos. De este sistema podría hallarse X.
En la práctica 2 vimos la operación de 'división izquierda' A\B, para resolver un sistema AX=B. Esta operación puede aplicarse cuando la matriz del sistema no es cuadrada o el sistema no tiene solución única y se obtiene una solución del sistema 'en el sentido de mínimos cuadrados'. Este mismo sentido es el que hemos descrito para hallar a y b, por lo que también podemos hallar X como A\B.
Veamos un ejemplo. Nos planteamos hallar la recta que ajusta los puntos (1, 2.7) , (2.1, 4.8) , (3 , 6.7) , (4 , 9.8) y (6 , 12.4) en el sentido de mínimos cuadrados. Comenzamos definiendo y representando los datos.
x=[1 ; 2.1 ; 3 ; 4 ; 6]
y=[2.7 ; 4.8 ; 6.7 ; 9.8 ; 12.4]
plot(x,y,'o')
x =
1.0000
2.1000
3.0000
4.0000
6.0000
y =
2.7000
4.8000
6.7000
9.8000
12.4000
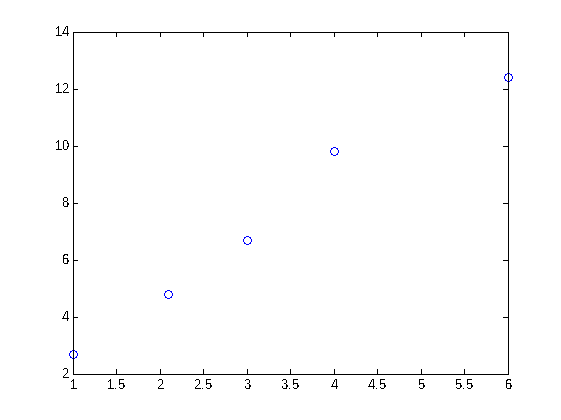
Planteamos el problema en la notación A*X=B.
m=length(y); A=[x , ones(m,1)] B=y
A =
1.0000 1.0000
2.1000 1.0000
3.0000 1.0000
4.0000 1.0000
6.0000 1.0000
B =
2.7000
4.8000
6.7000
9.8000
12.4000
Hallamos X usando la 'división izquierda'.
X=A\B a=X(1) b=X(2)
X =
2.0093
0.8099
a =
2.0093
b =
0.8099
Representamos la recta que ajusta los datos, y = a * x + b .
xd=[0:7];
yd=a*xd+b;
plot(x,y,'o',xd,yd)
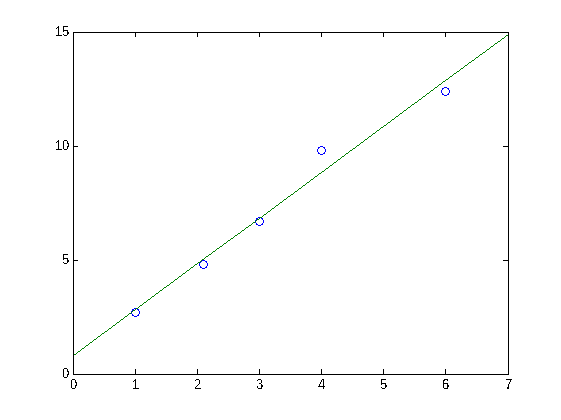
Comprobamos que el vector hallado X es (salvo errores de redondeo) solución del sistema transpose(A)*A*X = transpose(A)*B. También comprobamos que la matriz de este sistema es regular.
transpose(A)*A*X - transpose(A)*B determinante=det( transpose(A)*A )
ans =
1.0e-013 *
0.2842
0.2132
determinante =
72.8400
Ej 1. La pérdida de trayecto radioeléctrico (path loss) se define como el cociente entre la potencia de transmisión (Pt) y la potencia recibida (Pr).
Se quiere hallar el exponente g en un modelo en el que la pérdida de trayecto depende únicamente de la distancia desde el trasmisor (d) según la fórmula Pr=Pt*K*(1/d)^g.
La siguiente tabla muestra unas medidas de M=Pr/Pt (en dB) para distintas distancias en metros. (Tabla 2.3, Wireless Communication, Andrea Goldsmith)
d 10 20 50 100 300
M -70 -75 -90 -110 -125
d=[10; 20; 50; 100; 300]; M=[-70; -75; -90; -110; -125];
i) Represente los datos de la tabla, considerando las distancias en el eje de abscisas y el valor de M en el eje de ordenadas.
ii) Defina el vector x como menos 10 por el logaritmo decimal de la distancia, y defina el vector y como M. Represente estos datos tomando x en el eje de abscisas e y en el de ordenadas. (En Matlab y en Octave, el logaritmo decimal, común o en base 10 se halla con la función log10).
iii) Realice el ajuste lineal de los valores de y frente a x. (Sol. y=3.9669*x-26.7440 )
iv) Suponga que se cumple la fórmula del ajuste, que y=M=10*log10(Pr/Pt) y que x=-10*log10(d), y opere para hallar el valor de g. (g=3.9669, K=10^(-26.7440/10) ).
v) Halle la potencia recibida suponiendo que Pt=1 mW y que la distancia es de 200 metros. ¿Cuál es la pérdida de trayecto en este caso? Observando la tabla ¿tiene sentido el signo que obtiene? (Sol. Pr=1.5762e-012 mW , PL=6.3443e+011 = 118.0239 dB )
Ajuste parabólico por mínimos cuadrados
Nos planteamos ahora el problema de hallar una parábola y = a*x^2 + b x + c que ajuste un conjunto de puntos del plano (x1, y1), (x2, y2), ..., (xm, ym).
x=[1 ; 2.1 ; 3 ; 4 ; 6]
y=[2.7 ; 4.8 ; 6.7 ; 9.8 ; 12.4]
plot(x,y,'o')
x =
1.0000
2.1000
3.0000
4.0000
6.0000
y =
2.7000
4.8000
6.7000
9.8000
12.4000
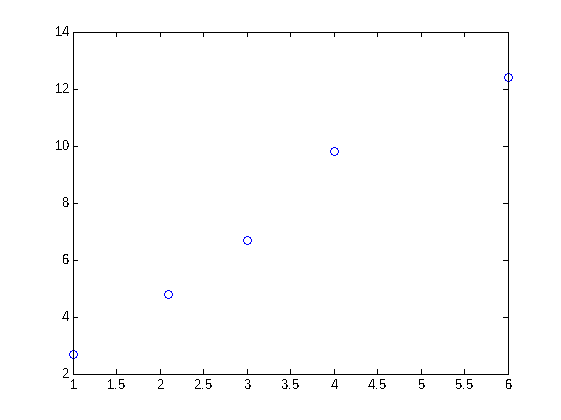
Si los puntos estuvieran sobre una parábola, podrían encontrarse valores a, b y c que serían una solución exacta del siguiente sistema lineal:
a x1^2 + b x1 + c = y1, a x2^2 + b x2 + c = y2, ... a xm^2 + b xm + c = ym.
Este sistema se puede expresar como A*X = B de forma matricial, definiendo
m=length(y); A=[x.^2 , x , ones(m,1)] B=y
A =
1.0000 1.0000 1.0000
4.4100 2.1000 1.0000
9.0000 3.0000 1.0000
16.0000 4.0000 1.0000
36.0000 6.0000 1.0000
B =
2.7000
4.8000
6.7000
9.8000
12.4000
Como en el caso anterior, aunque el sistema A*X=B sea incompatible, podemos hallar X usando la 'división izquierda' y obtener la solución 'en el sentido de los mínimos cuadrados'.
X=A\B a=X(1) b=X(2) c=X(3)
X =
-0.1050
2.7546
-0.1955
a =
-0.1050
b =
2.7546
c =
-0.1955
Representamos los datos junto con la parábola de ajuste.
xd=[0:0.1:7];
yd=a*xd.^2+b*xd+c;
plot(x,y,'o',xd,yd)
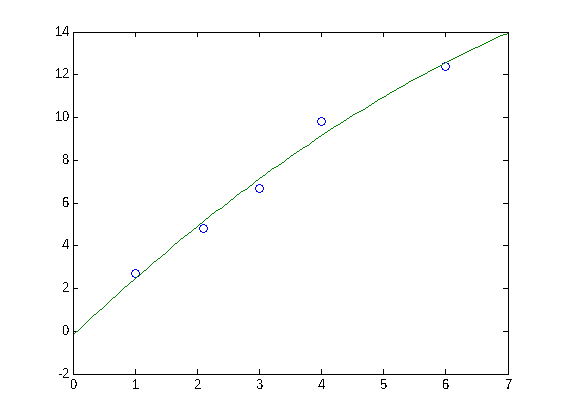
Ej 2. Para aplicar un filtro de cinco puntos a una señal, se quiere hallar la parábola que mejor ajusta los siguientes datos
t -2 -1 0 1 2
z 3 -1 2 1 3
i) Represente los datos de la tabla considerando los valores de t en el eje de abscisas (tiempo) y los valores de z en el eje de ordenadas (valor de la señal).
ii) Halle la parábola que mejor ajusta los datos de la tabla en el sentido de los mínimos cuadrados. (z(t)=0.5714*t^2+0.2*t+0.4571).
iii) Represente conjuntamente los datos de la tabla y la parábola obtenida.
iv) Halle el valor mínimo de la parábola obtenida. ¿Toma la señal algún valor por debajo del mínimo obtenido? ( zm=0.4396 )
Gráfica e integral definida de una expresión simbólica
Para el ajuste por mínimos cuadrados continuos necesitaremos hallar la integral definida de una expresión simbólica y usaremos la gráfica de una función simbólica para representar los resultados.
Comenzamos definiendo la variable simbólica x. También definimos una expresión simbólica f.
syms x
f=x^2+x+2
f = x^2+x+2
Usamos el comando ezplot para representar f en el intervalo [-3,4] .
ezplot(f , [-3,4] )
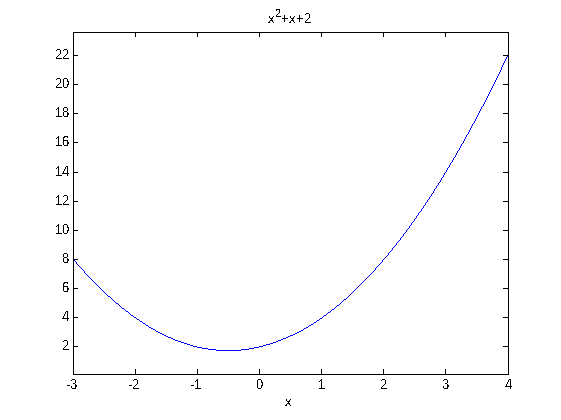
Ahora hallamos la integral definida en el mismo intervalo [-3,4]. Observe que obtenemos el valor exacto.
int( f, -3, 4 )
ans = 287/6
Ej 3. Represente la función g(x)=x^2-cos(x) en el intervalo [-pi, pi]. Halle la integral definida de g en ese mismo intervalo. (Sol. (2/3)*pi^3 ).
Mejor aproximación por mínimos cuadrados continua
En este problema la aproximación se hace dentro del espacio vectorial C([a,b]) de funciones reales continuas definidas en el intervalo [a, b]. En este espacio el producto escalar de dos funciones es la integral definida del producto de las dos funciones.
No podremos obtener la matriz del sistema (Gram) como en el caso anterior, sino que la hallaremos elemento a elemento.
Para ilustrar el proceso, hallaremos la mejor aproximación de la función f(x)=x^3 en el espacio generado por las funciones { v1, v2, v3 }= { 1, x, x^2 }. Obtendremos la mejor aproximación en el espacio de las funciones continuas definidas en el intervalo [-1, 1].
syms x
f=x^3;
v=[1,x,x^2]
a=-1;
b=1;
v = [ 1, x, x^2]
Inicializamos la matriz del sistema A y el término independiente B.
n=length(v); A=zeros(n,n); B=zeros(n,1);
Primero rellenamos el vector B con los productos de f por las funciones de la base.
for i=1:n B(i)=int( v(i)*f, a, b ); end
Rellenamos la matriz A (Gram) que contiene las integrales de v(i) por v(j) sabiendo que es simétrica.
for i=1:n for j=i+1:n A(i,j)=int( v(i)*v(j), a, b ); A(j,i)=A(i,j); end A(i,i)=int( v(i)*v(i), a, b ); end
Resolvemos el sistema y obtenemos los coeficientes de la combinación lineal que nos da la mejor aproximación.
coef=A\B mejor_aproximacion=v*coef
coef =
0
0.6000
0
mejor_aproximacion =
3/5*x
Para concluir, representamos simultáneamente la mejor_aproximación hallada junto con la función f que hemos aproximado.
ezplot( mejor_aproximacion , [a,b] ) hold on ezplot( f , [a,b] ) hold off
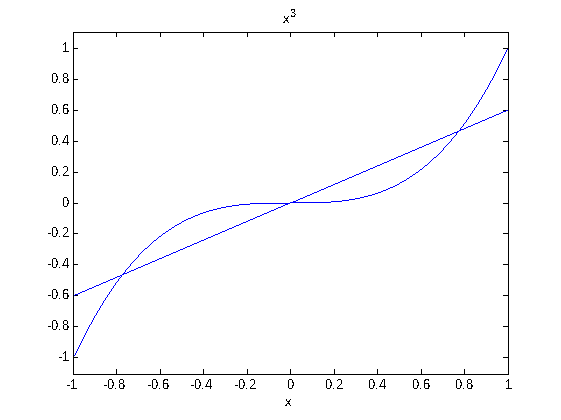
Ej 4. Considere el conjunto de funciones { 1, sin(x), cos(x), sin(2*x), cos(2*x), sin(3*x), cos(3*x) } y la función f(x)=x. i) Halle en C([-pi,pi]) la mejor aproximación de f al espacio lineal generado por el conjunto de funciones. ¿Cuál es la dimensión de dicho espacio lineal? (Sol. 2*sin(x)-sin(2*x)+2/3*sin(3*x) ).
ii) Represente conjuntamente la función f y la mejor aproximación obtenida.
iii) ¿Obtiene una matriz de Gram diagonal? ¿Es la matriz identidad? ¿Qué puede deducirse del conjunto de funciones empleado?
% Ecuaciones Diferenciales y Cálculo Numérico. (A. Palomares) % Grado en Ingeniería de Tecnologías de Telecomunicación. disp(date)
17-May-2023