Práctica 9. Mínimos cuadrados
En esta práctica veremos cómo hallar con MatLab, de dos formas distintas, la recta y la parábola que ajustan por mínimos cuadrados un conjunto de puntos del plano. La primera forma consiste en hallar el sistema formado por las ecuaciones normales del ajuste y resolverlo. La segunda, consiste en utilizar 'la división izquierda' de MatLab sobre un sistema A*X=B en el que A no es una matriz cuadrada.
Contents
Ajuste lineal por mínimos cuadrados
Dado un conjunto D de m puntos del plano (x1, y1), (x2, y2),..., (xm, ym) (o nube de puntos) con m>2, queremos hallar una recta y = a0+a1*x que 'pase lo más cerca posible' de esos puntos. Más concretamente, queremos hallar valores a0 y a1 que hagan que a0+a1*xi esté cerca de yi con i=1,..m, en el sentido de que la suma con i=1,...m de los valores (a0+a1*xi - yi)^2 sea la mínima posible. Tales valores a0 y a1 existen y son únicos y, por tanto, determinan una única recta en el plano. A dicha recta se la conoce como recta de mínimos cuadrados que ajusta D.
Para encontrar los valores a0 y a1 que determinan la recta y = a0 + a1 x de mínimos cuadrados que ajusta D hay que resolver un sistema de ecuaciones lineales compatible determinado que es el sistema formado por las ecuaciones normales de este ajuste (véanse los apuntes de teoría). Dicho sistema se puede escribir del siguiente modo (compruébalo):
M*transpose(M)*C = M*Y
donde:
M=[[1,...,1];[x1,...,xm]]
transpose(M) representa en MatLab la matriz transpuesta de la matriz M
C=[a0;a1] ,
Y=[y1;...;ym].
Veamos un ejemplo. Nos planteamos hallar la recta de mínimos cuadrados que ajusta los puntos (1, 2.7) , (2.1, 4.8) , (3 , 6.7) , (4 , 9.8) y (6 , 12.4).
Comenzamos representando gráficamente los puntos que hay que ajustar.
x=[1 2.1 3 4 6]
y=[2.7 4.8 6.7 9.8 12.4]
plot(x,y,'or')
x =
1.0000 2.1000 3.0000 4.0000 6.0000
y =
2.7000 4.8000 6.7000 9.8000 12.4000

Hallamos el sistema de las ecuaciones normales del ajuste lineal por mínimos cuadrados de dichos puntos (su matriz de coeficientes y su vector de términos independientes).
m=length(x); M=[ones(1,m);x]; disp('Matriz de coeficientes del sistema de las ecuaciones normales del ajuste :') disp(M*transpose(M)) Y=transpose(y); disp('Vector de términos independientes del sistema de las ecuaciones normales del ajuste :') disp(M*Y)
Matriz de coeficientes del sistema de las ecuaciones normales del ajuste :
5.0000 16.1000
16.1000 66.4100
Vector de términos independientes del sistema de las ecuaciones normales del ajuste :
36.4000
146.4800
Resolvemos el sistema de las ecuaciones normales usando, por comodidad, la división izquierda (antes comprobamos que la matriz de coeficientes de dicho sistema es regular). Las componentes del vector solución de dicho sistema son los coeficientes de la recta de mínimos cuadrados que ajusta los puntos dados.
det(M*transpose(M)) % Resolvemos el sistema de las ecuaciones normales usando la división izquierda C=(M*transpose(M))\(M*Y) disp('Los coeficientes de la recta y=a0+a1*x son : ') a0=C(1) a1=C(2)
ans =
72.8400
C =
0.8099
2.0093
Los coeficientes de la recta y=a0+a1*x son :
a0 =
0.8099
a1 =
2.0093
Hallamos el número de condición de la matriz de coeficientes del sistema con la norma 2 (la matriz de coeficientes del sistema de las ecuaciones normales del ajuste puede estar mal condicionada, lo que puede provocar que al resolver dicho sistema con el ordenador el vector solución, C, que se obtiene se vea distorsionado por los errores de redondeo).
cond(M*transpose(M),2)
ans = 67.9934
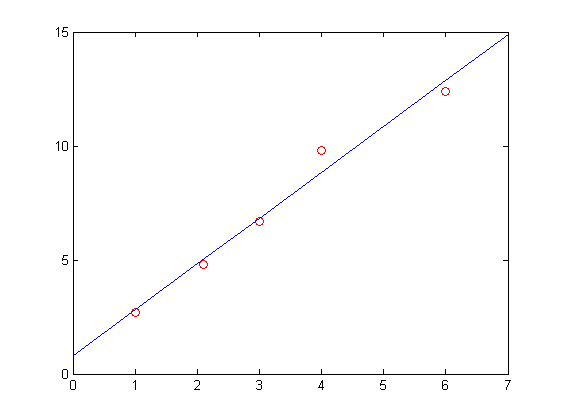
Por último, representamos gráficamente los puntos (en rojo) y la recta de mínimos cuadrados que los ajusta (en azul).
xd=[0:7]; yd=a0+a1*xd; plot(x,y,'or',xd,yd,'b')
Con MatLab también se puede hallar la recta de mínimos cuadrados y = a0+a1*x que ajusta los puntos (x1, y1), (x2, y2),..., (xm, ym), con m>2, usando la 'división izquierda' sobre el sistema A*X=B , donde:
A=[[x1 1];[x2 1];...;[xm 1]]
X=[a1;a0] ,
B=[y1;...;ym].
Observe que la matriz A no es una matriz cuadrada, y que si los puntos (x1, y1), (x2, y2),..., (xm, ym) no están alineados entonces el sistema A*X=B es incompatible.
Las componentes del vector X que se obtiene al usar la 'división izquierda' sobre A*X=B son los coeficientes de la recta de mínimos cuadrados que ajusta los puntos dados (observe que éstos aparecen en orden inverso a como aparecían en el vector C que se obtuvo al resolver el sistema de las ecuaciones normales del ajuste).
Con este modo de hallar la recta de mínimos cuadrados y = a0+a1*x no se obtiene el sistema de las ecuaciones normales del ajuste.
A continuación aparece el código de MatLab correspondiente a esta segunda forma de hallar la recta de mínimos cuadrados y = a0+a1*x que ajusta los puntos (x1, y1), (x2, y2),..., (xm, ym), con m>2 :
x=[1 2.1 3 4 6];
y=[2.7 4.8 6.7 9.8 12.4];
m=length(x);
A=[transpose(x),ones(m,1)]
B=transpose(y)
X=A\B
disp('Los coeficientes de la recta y=a0+a1*x son : ')
a0=X(2)
a1=X(1)
A =
1.0000 1.0000
2.1000 1.0000
3.0000 1.0000
4.0000 1.0000
6.0000 1.0000
B =
2.7000
4.8000
6.7000
9.8000
12.4000
X =
2.0093
0.8099
Los coeficientes de la recta y=a0+a1*x son :
a0 =
0.8099
a1 =
2.0093
Ej 1. En la oxidación del dióxido de azufre se obtiene trióxido de azufre. La siguiente tabla muestra los valores de Kep (constante de equilibrio termodinámica para gases) de la reacción
2 SO2 + O2 <--> 2 SO3
para distintas temperaturas en grados Kelvin. (Tabla 20.3, Química General, Petrucci)
T 800 850 900 950 1000 1050 1100 1170 Kep 9.1e2 1.7e2 4.2e1 1.0e1 3.2 1.0 3.9e-1 1.2e-1
i) Represente gráficamente en color rojo los datos de la tabla, considerando las temperaturas en el eje de abscisas y los valores de Kep en el eje de ordenadas.
ii) Defina un vector x cuyas componentes son los inversos de los valores de las temperaturas y un vector y cuyas componentes son los logaritmos neperianos de los valores de las constantes de equilibrio. Represente gráficamente en color azul el conjunto D de los puntos del plano cuyas abscisas y ordenadas son, respectivamente, las componentes de los vectores x e y.
iii) Halle la recta que ajusta por mínimos cuadrados D. (Sol. y= - 21.5809 + 2.2722e+004 * x )
iv) Halle las ecuaciones normales del ajuste del apartado anterior (antes de calcularlas ejecute primero el comando format long y cuando termine de resolver el apartado vuelva al formato inicial ejecutando format short). (Sol. Matriz de coeficientes= [[8.000000000000000 0.008306385994466]; [0.008306385994466 0.000008753173498]] Vector de términos independientes=[16.090776481585713;0.019630613572036])
v) Sabiendo que la constante de equilibrio termodinámica (Keq), la entalpía de la reacción (VH) y la variación de la entalpía (VS) cumplen la siguiente ecuación
- VH 1 VS
ln Keq = --------- * --- + --------
R T Rdonde R es la constante de los gases, R= 8.3145 J /(mol * K), determine la entalpía de la reacción suponiendo que x=1/T, e y=ln Keq. (Sol. Entalpía de la reacción = -1.8892e+005 J/mol) .
T = [800 850 900 950 1000 1050 1100 1170]; Kep=[9.1e2 1.7e2 4.2e1 1.0e1 3.2 1.0 3.9e-1 1.2e-1] ;
Ajuste parabólico por mínimos cuadrados
Dado un conjunto D de m puntos del plano (x1, y1), (x2, y2),..., (xm, ym) (o nube de puntos) con m>3, queremos hallar una parábola y = a0+a1*x+a2*x^2 que 'pase lo más cerca posible' de esos puntos. Más concretamente, queremos encontrar valores a0, a1 y a2 que hagan que a0+a1*xi+a2*xi^2 esté cerca de yi con i=1,..m, en el sentido de que la suma con i=1,...m de los valores (a0+a1*xi+a2*xi^2 - yi)^2 sea la mínima posible. Tales valores a0, a1 y a2 existen y son únicos y, por tanto, determinan una única parábola en el plano. A dicha parábola se la conoce como parábola de mínimos cuadrados que ajusta D.
Para encontrar los valores a0, a1 y a2 que determinan la parábola y = a0+a1*x+a2*x^2 de mínimos cuadrados que ajusta D hay que resolver un sistema de ecuaciones lineales compatible determinado que es el sistema formado por las ecuaciones normales de este ajuste (véanse los apuntes de teoría). Dicho sistema se puede escribir del siguiente modo (compruébalo):
M*transpose(M)*C = M*Y
donde:
M=[[1,...,1];[x1,...,xm];[x1^2,x2^2,...,xm^2]]
transpose(M) representa en MatLab la matriz transpuesta de la matriz M
C=[a0;a1;a2] ,
Y=[y1;...;ym].
Veamos un ejemplo. Nos planteamos hallar la parábola de mínimos cuadrados que ajusta los puntos (1, 2.7) , (2.1, 4.8) , (3 , 6.7) , (4 , 9.8) y (6 , 12.4).
Recordamos la representación gráfica de los puntos que hay que ajustar (ya se vió en el apartado anterior de la práctica).
x=[1 2.1 3 4 6]
y=[2.7 4.8 6.7 9.8 12.4]
plot(x,y,'or')
x =
1.0000 2.1000 3.0000 4.0000 6.0000
y =
2.7000 4.8000 6.7000 9.8000 12.4000

Hallamos el sistema de las ecuaciones normales del ajuste parabólico por mínimos cuadrados de dichos puntos (su matriz de coeficientes y su vector de términos independientes).
m=length(x); M=[ones(1,m);x;x.^2]; disp('Matriz de coeficientes del sistema de las ecuaciones normales del ajuste :') disp(M*transpose(M)) Y=transpose(y); disp('Vector de términos independientes del sistema de las ecuaciones normales del ajuste :') disp(M*Y)
Matriz de coeficientes del sistema de las ecuaciones normales del ajuste :
1.0e+03 *
0.0050 0.0161 0.0664
0.0161 0.0664 0.3173
0.0664 0.3173 1.6534
Vector de términos independientes del sistema de las ecuaciones normales del ajuste :
36.4000
146.4800
687.3680
Resolvemos el sistema de las ecuaciones normales usando, por comodidad, la división izquierda (antes comprobamos que la matriz de coeficientes de dicho sistema es regular). Las componentes del vector solución de dicho sistema son los coeficientes de la parábola de mínimos cuadrados que ajusta los puntos dados.
det(M*transpose(M)) % Resolvemos el sistema de las ecuaciones normales usando la división izquierda C=(M*transpose(M))\(M*Y) disp('Los coeficientes de la parábola y=a0+a1*x+a2*x^2 son : ') a0=C(1) a1=C(2) a2=C(3)
ans =
2.7088e+03
C =
-0.1955
2.7546
-0.1050
Los coeficientes de la parábola y=a0+a1*x+a2*x^2 son :
a0 =
-0.1955
a1 =
2.7546
a2 =
-0.1050
Hallamos el número de condición de la matriz de coeficientes del sistema con la norma 2 (la matriz de coeficientes del sistema de las ecuaciones normales del ajuste puede estar mal condicionada, lo que puede provocar que al resolver dicho sistema con el ordenador el vector solución, C, que se obtiene se vea distorsionado por los errores de redondeo).
cond(M*transpose(M),2)
ans = 8.0597e+03
Por último, representamos gráficamente los puntos (en rojo) y la parábola de mínimos cuadrados que los ajusta (en verde).
xd=[0:7]; yd=a0+a1*xd+a2*xd.^2; plot(x,y,'or',xd,yd,'g')

Con MatLab también se puede hallar la parábola de mínimos cuadrados y = a0+a1*x+a2*x^2 que ajusta los puntos (x1, y1), (x2, y2),..., (xm, ym), con m>2, usando la 'división izquierda' sobre el sistema A*X=B , donde:
A=[[x1^2 x1 1];[x2^2 x2 1];...;[xm^2 xm 1]]
X=[a2;a1;a0] ,
B=[y1;...;ym].
Observe que la matriz A no es una matriz cuadrada, y que si los puntos (x1, y1), (x2, y2),..., (xm, ym) no están situados sobre una parábola entonces el sistema A*X=B es incompatible.
Las componentes del vector X que se obtiene al usar la 'división izquierda' sobre A*X=B son los coeficientes de la parábola de mínimos cuadrados que ajusta los puntos dados (observe que éstos aparecen en orden inverso a como aparecían en el vector C que se obtuvo al resolver el sistema de las ecuaciones normales del ajuste).
Con este modo de hallar la parábola de mínimos cuadrados y=a0+a1*x+a2*x^2 no se obtiene el sistema de las ecuaciones normales del ajuste.
A continuación aparece el código de MatLab correspondiente a esta segunda forma de hallar la parábola de mínimos cuadrados y = a0+a1*x+a2*x^2 que ajusta los puntos (x1, y1), (x2, y2),..., (xm, ym), con m>3 :
x=[1 2.1 3 4 6];
y=[2.7 4.8 6.7 9.8 12.4];
m=length(x);
A=[transpose(x.^2),transpose(x),ones(m,1)]
B=transpose(y)
X=A\B
disp('Los coeficientes de la parábola y=a0+a1*x+a2*x^2 son : ')
a0=X(3)
a1=X(2)
a2=X(1)
A =
1.0000 1.0000 1.0000
4.4100 2.1000 1.0000
9.0000 3.0000 1.0000
16.0000 4.0000 1.0000
36.0000 6.0000 1.0000
B =
2.7000
4.8000
6.7000
9.8000
12.4000
X =
-0.1050
2.7546
-0.1955
Los coeficientes de la parábola y=a0+a1*x+a2*x^2 son :
a0 =
-0.1955
a1 =
2.7546
a2 =
-0.1050
Ej 2. La siguiente tabla muestra el número atómico y el radio atómico en picómetros de los metales de la primera serie de transición, salvo el Vanadio (Tabla 24.1, Química General, Petrucci).
Elemento Sc Ti Cr Mn Fe Co Ni Cu Zn Número atómico 21 22 24 25 26 27 28 29 30 Radio metálico 161 145 125 124 124 125 128 128 133
i) Halle la parábola que ajusta por mínimos cuadrados los puntos del plano que se obtienen tomando en el eje de abscisas los números atómicos y en el de ordenadas los radios metálicos. (Sol. y = 934.1174 - 61.0538*x + 1.1477*x^2 )
ii) Represente gráficamente en el intervalo [20,32] los puntos del apartado anterior (en azul) junto con la parábola de mínimos cuadrados que los ajusta (en verde).
iii) Suponga que tal parábola puede usarse para estimar el radio atómico del Vanadio (número atómico 23). ¿Qué error relativo se estaría cometiendo al considerar dicha estimación si el radio atómico del Vanadio es 132? (Sol. Radio estimado = 137.0093, error relativo = -0.0379).
x=[ 21 22 24 25 26 27 28 29 30];
y=[ 161 145 125 124 124 125 128 128 133];
% Matemáticas II. Grado en Ingeniería Química. (A. Palomares)
disp(date)
19-Apr-2017