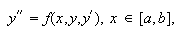 siendo
siendo
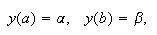 o, en general, del tipo
o, en general, del tipo 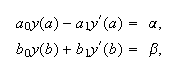 con
con Un problema de contorno para una ecuación diferencial es aquel en el que a la
variable dependiente o incógnita se le exigen condiciones en dos o más puntos
distintos. Nos centraremos en los problemas de contorno para ecuaciones
diferenciales lineales de segundo orden, es decir, problemas del tipo 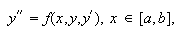 siendo
siendo
![]() y
y ![]() , con condiciones del tipo
, con condiciones del tipo
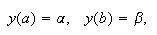 o, en general, del tipo
o, en general, del tipo 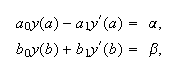 con
con ![]() y
y ![]() .
.
Del mismo modo que ocurre para problemas de valores iniciales, sólo una minoría de ecuaciones lineales pueden resolverse mediante métodos que aparecen en las obras dedicadas a su estudio. Por otro lado, no siempre es posible explicitar una solución que verifique ciertas condiciones del tipo (c16:e2) o, en general, del tipo (c16:e3). Es por ello que se hace necesaria, en la práctica la aplicación de métodos numéricos de resolución aproximada.
Entre los m\as conocidos y utilizados se encuentran el m\etodo de tiro, el de diferencias finitas, los m\etodos de Ritz y Galerkin, o los m\etodos tipo spline entre los que destaca el m\etodo de los elementos finitos.
En este capítulo nos centraremos en los dos primeros: el m\etodo de tiro y el m\etodo de diferencias finitas. Los restantes ser\an objeto de estudio en posteriores capítulos.
Consideremos el problema de contorno (c16:e1 )--(c16:e2). Nos proponemos estudiar, en principio, bajo qué condiciones podemos asegurar la existencia y unicidad de solución para este problema. Especial atención merecerá el caso en el que la ecuación diferencial (c16:e1) sea lineal.
Para las demostraciones de los resultados que a continuación enunciamos así como para un estudio más especializado en problemas de contorno y sus métodos numéricos, pueden consultarse los libros de Keller y Burden, entre otros.
![]() ,
, ![]() y
y ![]() son continuas
en
son continuas
en ![]() ,
,
![]() para
todo
para
todo ![]() ,
,
existe una constante ![]() tal que
tal que 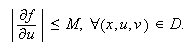
Entonces el problema (c16:e1 )--(c16:e2) tiene solución única.
En particular, como consecuencia de este teorema, se obtiene el siguiente
resultado para el caso en que la ecuación diferencial (c16:e1) sea lineal, es decir, si ![]() , para
, para ![]() .
.
![]() ,
, ![]() y
y ![]() son continuas en
son continuas en ![]()
![]() para
todo
para
todo ![]() ,
,
entonces el problema (c16:e4) tiene solución única.
Vamos es estudiar un método de aproximación de la solución de un problema de contorno lineal de la forma (c16:e4), o más general, de la forma (c16:e1 )--(c16:e2), que en las condiciones del corolario c16:cor1 o del teorema c16:teo1, respectivamente, existe y es única, mediante la resolución de problemas de valores iniciales asociados a los mismos.
Nos ocupamos en principio del problema lineal. Por tanto, consideremos el
problema de contorno (c16:e4) y supongamos que se
verifican las condiciones del corolario c16:cor1.
Asociados a este problema, consideremos los problemas de valores iniciales 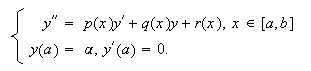 y
y
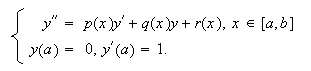
Bajo las condiciones del corolario c16:cor1, los
problemas (c16:e5) y (c16:e6 )
admiten soluciones únicas, definidas en ![]() .
.
Supongamos que se verifican las hipótesis del
corolario c16:cor1. Sean ![]() e
e ![]() las únicas
soluciones de los problemas (c16:e5) y (c16:e6), respectivamente. Entonces
las únicas
soluciones de los problemas (c16:e5) y (c16:e6), respectivamente. Entonces 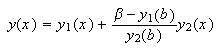 es la única solución del
problema (c16:e4).
es la única solución del
problema (c16:e4).
Demostración.- Bajo las hipótesis del corolario c16:cor1, se verifica que ![]() y, por tanto,
y, por tanto, ![]() está bien definida por (c16:e7). Además,
está bien definida por (c16:e7). Además, 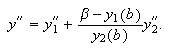 Teniendo en cuenta que
Teniendo en cuenta que ![]() es la solución
de (c16:e5) e
es la solución
de (c16:e5) e ![]() lo es de (c16:e6), se sigue que
lo es de (c16:e6), se sigue que 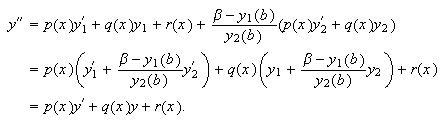 Además se verifica que
Además se verifica que 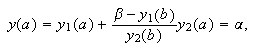 y
y
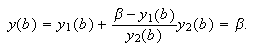 Luego
Luego ![]() es la única solución de
(c16:e4 ).
es la única solución de
(c16:e4 ). ![]()
El método de tiro para el problema de contorno (c16:e4) consiste, por tanto, en hallar una aproximación del
problema de valores (c16:e5), otra del (c16:e6), y construir la solución ![]() dada por (c16:e7), tal y como se indica en el siguiente algoritmo:
dada por (c16:e7), tal y como se indica en el siguiente algoritmo:
| ALGORITMO DEL MÉTODO DE TIRO LINEAL |
| Entrar |
| Hallar |
| mediante un método numérico para problemas de valores iniciales |
| Hallar |
| mediante un método numérico para problemas de valores iniciales |
| Escribir |
En los pasos segundo y tercero de este algoritmo se necesita incluir el algoritmo de alguno de los métodos de resolución aproximada de problemas de valores iniciales estudiados en el capítulo anterior, tanto para el problema (c16:e5) como para el (c16:e6). El error del método de tiro para problemas lineales vendrá determinado por el error del método de aproximación empleado para estos problemas de valores iniciales, ya que la construcción de la solución del primero es lineal con respecto a las soluciones de los otros dos.
Consideremos ahora el caso general de un problema de contorno de segundo
orden, no necesariamente lineal. Es decir, se trata del problema de contorno
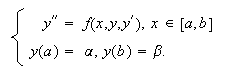
En este caso, la soluci\on del problema no puede expresarse como una
combinaci\on lineal de las soluciones de dos problemas de valores iniciales,
debido a la no linealidad de ![]() . Para hallarla har\a falta
realizar un proceso iterativo.
. Para hallarla har\a falta
realizar un proceso iterativo.
Consideremos el problema de valores iniciales 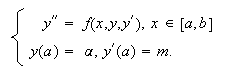 para un cierto valor de
para un cierto valor de
![]() dado, que indicará
la pendiente de salida de la solución del problema (de ahí el nombre de método
de tiro).
dado, que indicará
la pendiente de salida de la solución del problema (de ahí el nombre de método
de tiro).
Sea ![]() la
solución de este problema. Coincidirá con la solución de (c16:e8) si
la
solución de este problema. Coincidirá con la solución de (c16:e8) si 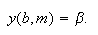
Por tanto, se trata de resolver (en la variable ![]() ) esta última ecuación,
para lo cual se puede aplicar cualquier método numérico de los estudiados en el
capítulo 2. Pero el empleo de un método u otro necesitará de un mayor o menor
conocimiento de la solución de (c16:e9) y, quizá, de
alguna derivada, lo cual puede hacer complicada su aplicación.
) esta última ecuación,
para lo cual se puede aplicar cualquier método numérico de los estudiados en el
capítulo 2. Pero el empleo de un método u otro necesitará de un mayor o menor
conocimiento de la solución de (c16:e9) y, quizá, de
alguna derivada, lo cual puede hacer complicada su aplicación.
Uno de los métodos más sencillos que se puede utilizar para resolver (c16:e10) es el método de la secante, para lo que se necesita
dar dos valores iniciales, ![]() y
y ![]() , y hallar las
siguientes aproximaciones mediante la iteración
, y hallar las
siguientes aproximaciones mediante la iteración 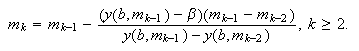
A continuación, conocido el valor de ![]() en la iteración
en la iteración ![]() --ésima, se vuelve a
resolver el problema (c16:e9) para
--ésima, se vuelve a
resolver el problema (c16:e9) para ![]() y, mediante
(c16:e11) para
y, mediante
(c16:e11) para ![]() , obtener un nuevo valor de
la pendiente del tiro
, obtener un nuevo valor de
la pendiente del tiro ![]() , reiterando el proceso
hasta que se verifique un cierto criterio de parada.
, reiterando el proceso
hasta que se verifique un cierto criterio de parada.
La convergencia del m\etodo de la secante, en condiciones adecuadas, asegura la convergencia del m\etodo de tiro no lineal.
Por tanto, el método de tiro, usando el método de la secante, consiste en hallar una solución aproximada de (c16:e8) mediante el siguiente algoritmo (en el que la variable niter indica el número de iteraciones que deseamos realizar):
| ALGORITMO DEL MÉTODO DE TIRO NO LINEAL (SECANTE) |
| Entrar |
| Hallar |
| de (c16:e9)
para |
| Hallar |
| de (c16:e9)
para |
| Para |
| Hallar |
| de (c16:e9)
para |
| Escribir |
Análogamente, se podría haber utilizado el método de Newton--Raphson para hallar una solución aproximada de (c16:e10) en cada iteración, pero la necesidad de conocer la derivada de la solución en la iteración anterior lleva consigo tener que resolver un nuevo problema de valores iniciales. Para un estudio más detallado del método en este caso puede consultarse el libro de Burden[ ], pp. 573--576.
Debido a la complejidad de estudio del error en estos m\etodos, no vamos a indicar nada sobre el mismo, pero un estudio detallado para el caso de condiciones m\as generales, así como para problemas de contorno para sistemas de ecuaciones diferenciales no lineales, puede realizarse consultando el libro de Keller[ ].
Los métodos de tiro, tanto para problemas lineales como no lineales, presentan problemas de inestabilidad. Para evitar esto se puede hacer uso de un método de diferencias finitas como los que describiremos a continuación, que, aunque son menos precisos que el método de tiro, presentan mayor estabilidad.
Estos m\etodos se basan en la sustituci\on de las derivadas que aparecen en el problema de contorno por f\ormulas de derivaci\on num\erica adecuadas, con el orden de error deseado.
Para ello, sea ![]() y consideremos en el
intervalo
y consideremos en el
intervalo ![]() una partición uniforme en
una partición uniforme en ![]() subintervalos, es decir,
la partición de nodos
subintervalos, es decir,
la partición de nodos 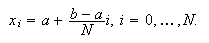
Sean ![]() ,
,
![]() ,
, ![]() valores reales
que suponemos que aproximan a
valores reales
que suponemos que aproximan a ![]() ,
, ![]() ,
, ![]() , siendo
, siendo ![]() la solución de un problema de contorno dado. Entonces, se sabe que, para
la solución de un problema de contorno dado. Entonces, se sabe que, para ![]() ,
,
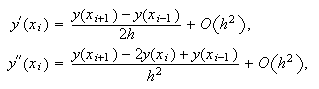 y, por tanto,
y, por tanto, 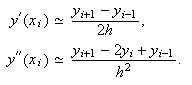
En el caso lineal, es decir, si consideramos el problema c16:e4, efectuando las aproximaciones antes indicadas, para
cada uno de los nodos interiores de la partición fijada, se obtienen las
igualdades 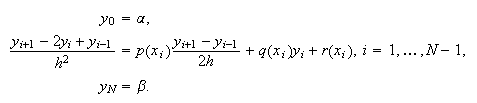 que se pueden escribir en forma
matricial como
que se pueden escribir en forma
matricial como 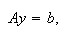 donde
donde ![]() ,
, 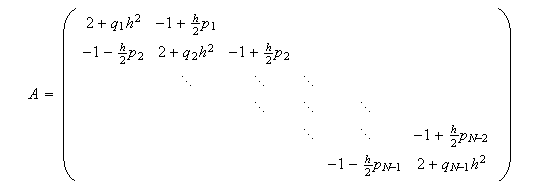 y
y
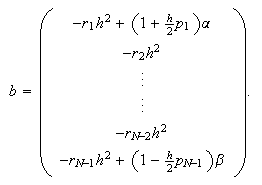 habiendo utilizado la notación
habiendo utilizado la notación
![]() ,
, ![]() y
y ![]() ,
, ![]() .
.
Por tanto, el algoritmo es el siguiente:
| ALGORITMO DEL MÉTODO DE DIFERENCIAS FINITAS LINEAL |
| Entrar |
| Para |
| Para |
| Resolver |
| Escribir |
Obsérvese que la salida del algoritmo es el vector de incógnitas ![]() . Por otra parte, la
resolución del sistema
. Por otra parte, la
resolución del sistema ![]() se puede hacer mediante
el método de descomposición
se puede hacer mediante
el método de descomposición ![]() para el caso de matrices
tridiagonales.
para el caso de matrices
tridiagonales.
Los siguientes resultados, cuya demostraci\on omitimos, establecen condiciones suficientes tanto para la unisolvencia de este sistema lineal, como para la determinaci\on de un orden de convergencia cuadr\atico.
Supongamos que ![]() y
y ![]() son continuas en
son continuas en ![]() y que
y que ![]() , para todo
, para todo ![]() . Sea
. Sea ![]() . Si
. Si ![]() entonces el sistema tridiagonal (c16:e12.1 )-(c16:e12.3) tiene una única solución.
entonces el sistema tridiagonal (c16:e12.1 )-(c16:e12.3) tiene una única solución.
Bajo las hipótesis del teorema anterior, sean ![]() la única solución de (c16:e4) e
la única solución de (c16:e4) e ![]() la única
solución de (c16:e12.1 )-(c16:e12.3). Si
la única
solución de (c16:e12.1 )-(c16:e12.3). Si ![]() entonces
entonces 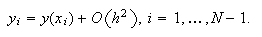
En el caso de un problema de contorno no lineal, éste se complica ya que el sistema de ecuaciones que se obtiene razonando como para el caso lineal no es lineal, por lo que deberá resolverse mediante alguno de los métodos numéricos de resolución de sistemas de ecuaciones no lineales estudiados en el capítulo 8, como, por ejemplo, el método de Newton.
Consideremos, por tanto, el problema de contorno no lineal (c16:e9). Aproximando, de nuevo, las derivadas que aparecen por
fórmulas de derivación numérica adecuadas y considerando que ![]() son aproximaciones de
son aproximaciones de
![]() ,
respectivamente, siendo
,
respectivamente, siendo ![]() la solución de (c16:e9), siempre que ésta exista, se obtiene el siguiente
sistema de ecuaciones, no necesariamente lineales:
la solución de (c16:e9), siempre que ésta exista, se obtiene el siguiente
sistema de ecuaciones, no necesariamente lineales: 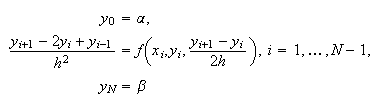
Aplicando el método de Newton para su resolución, se puede probar que el
método es convergente de orden ![]() (véase Isaacson y
Keller).
(véase Isaacson y
Keller).
Estos métodos numéricos nos servirán para aproximar tanto la extremal de un funcional como la solución de un problema de contorno autoadjunto asociado. Como veremos, el método de Galerkin nos permitirá también tratar problemas no autoadjuntos, que no provienen directamente de la optimización de un funcional. Por ello su uso está bastante extendido para todo tipo de problemas diferenciales e integrales, sobre todo de tipo lineal, en los que se requiere determinar una cierta función solución, que juega el papel de incógnita, y que es la que queremos aproximar.
La idea en todo caso es la de reemplazar el espacio de funciones de dimensión infinita donde se plantea el problema original por otros espacios de dimensión finita, que estarán generados por funciones que verifiquen además, ciertas condiciones de contorno exigidas.
Estas funciones del espacio de dimensión finita podrán estar definidas de manera global y tener soporte repartido por todo el intervalo considerado (siendo principalmente de tipo polinómico con grado creciente o bien trigonométrico) o a trozos (a partir de la correspondiente partición del intervalo de partida) conformando los conocidos splines (lineales, cuadráticos o cúbicos, principalmente).
Las funciones de base ser ortogonales respecto a cierto producto escalar conveniente en el espacio de funciones considerado o casi-ortogonales, por ejemplo si las funciones de base tienen un soporte muy localizado.
La idea de considerar funciones polinómicas definidas a trozos sobre una partición cada vez más fina. Éstos incluyen los denominados métodos de elementos finitos, en los que se exige cierta regularidad a las funciones del espacio resultante.
La base pues de todos estos métodos radica en una buena elección de una
sucesión de funciones, llamadas funciones coordenadas, que
formen un sistema independiente del espacio de funciones considerado, y que sea
un conjunto denso del mismo, en el sentido de que el
conjunto de combinaciones lineales finitas de éstas permita aproximar con la
exactitud deseada cualquier función del espacio donde se debe encontrar la
verdadera solución. No obstante, esta idea intuitiva de aproximación,
necesitaría muchos de los conceptos fundamentales del Análisis Funcional moderno
para poder formularse desde un marco matemático riguroso. Así pues, cabe
considerar el concepto de espacio métrico de funciones, en
el que se tiene una determinada distancia, ![]() . Este espacio se dirá que
es completo cuando todas las sucesiones de Cauchy sean
convergentes hacia una función de dicho espacio (repasar por ejemplo los
conceptos equivalentes en el cuerpo completo de los números reales); en
particular, se podrán considerar los denominados espacios de
Banach, en los que dicha distancia proviene de una determinada norma, o
los llamados espacios de Hilbert, en los que la norma
proviene a su vez de un producto escalar.
. Este espacio se dirá que
es completo cuando todas las sucesiones de Cauchy sean
convergentes hacia una función de dicho espacio (repasar por ejemplo los
conceptos equivalentes en el cuerpo completo de los números reales); en
particular, se podrán considerar los denominados espacios de
Banach, en los que dicha distancia proviene de una determinada norma, o
los llamados espacios de Hilbert, en los que la norma
proviene a su vez de un producto escalar.
En cualquiera de estos casos, lo fundamental además es que en dicho espacio
sea posible encontrar una sucesión de funciones coordenadas (linealmente
independientes), ![]() , tal que, si
, tal que, si ![]() es
el subespacio vectorial de
es
el subespacio vectorial de ![]() generado por las
generado por las ![]() primeras funciones
coordenadas,
primeras funciones
coordenadas, ![]() , se
verifiquen las siguientes propiedades:
, se
verifiquen las siguientes propiedades:
Aquí, ![]() es la adherencia o cierre
topológico del conjunto
es la adherencia o cierre
topológico del conjunto ![]() según la distancia
considerada en dicho espacio.
según la distancia
considerada en dicho espacio.
Cuando estemos considerando un espacio de funciones ![]() le pediremos a esta
sucesión de funciones coordenadas que ve-ri-fi-que la siguiente propiedad: para
cualesquiera
le pediremos a esta
sucesión de funciones coordenadas que ve-ri-fi-que la siguiente propiedad: para
cualesquiera ![]() e
e ![]() existen números reales
existen números reales
![]() ,
, ![]() ,
, ![]() ,
, ![]() tales que la
función
tales que la
función ![]() cumple
que
cumple
que 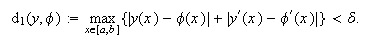
![]() es la distancia usual en
el espacio de funciones de clase
es la distancia usual en
el espacio de funciones de clase ![]() .
.
Basándonos en el conocido teorema de Weierstrass, de aproximación de funciones suficientemente diferenciables mediante polinomios, o bien en los teoremas de representación de funciones mediante series de Fourier trigonométricas, es fácil justificar que los siguientes sistemas de funciones polinómicas o trigonométricas, dependientes del tipo de condiciones de contorno, verifican las propiedades necesarias.
Para condiciones de Dirichlet homogéneas ![]()
de tipo polinómico 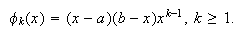
de tipo trigonométrico 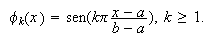
Para condiciones de Neumann homogéneas ![]()
de tipo polinómico 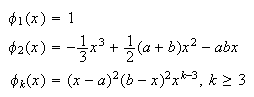
de tipo trigonométrico 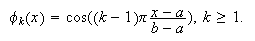
Para las condiciones mixtas ![]()
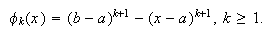
Para las condiciones mixtas ![]()
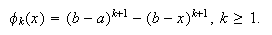
Otra cuestión de vital importancia al respecto radica en el hecho de que el buen o mal condicionamiento del problema discreto resultante puede depender también en gran medida de las propiedades de ortogonalidad o casi-ortogonalidad de dichas funciones de base. Por ello, en algunos problemas más complejos será conveniente usar sistemas de funciones especiales, como sistemas de polinomios ortogonales o funciones de Bessel.
Por ejemplo, los denominados polinomios generalizados de
Jacobi, ![]() . Incluyen como caso
particular a los conocidos polinomios de Legendre (que
corresponden a
. Incluyen como caso
particular a los conocidos polinomios de Legendre (que
corresponden a ![]() ) y verifican la propiedad
de ortogonalidad
) y verifican la propiedad
de ortogonalidad 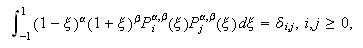 que puede ser aprovechada para
realizar desarrollos del tipo
que puede ser aprovechada para
realizar desarrollos del tipo ![]() o bien para tomar como
base, por ejemplo, la constituida por las funciones
o bien para tomar como
base, por ejemplo, la constituida por las funciones 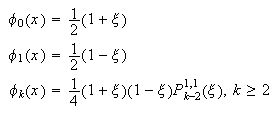
Este método también se conoce con el nombre de Rayleigh-Ritz, ya que es una generalización que ideó Ritz en 1908 de una técnica que Lord Rayleigh (1877-1878) ya había aplicado en su trabajo Theory of Sounds para calcular de forma aproximada los valores propios de ciertos problemas que surgen al estudiar las vibraciones de láminas y placas. También aplicaremos este método para encontrar aproximaciones de las soluciones de problemas de Sturm-Liouville en un capítulo posterior.
Se puede aplicar por ejemplo, para aproximar las extremales del funcional
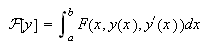 definido en un espacio de
funciones
definido en un espacio de
funciones ![]() , donde se tiene unas condiciones de contorno, no necesariamente
homogéneas, siendo
, donde se tiene unas condiciones de contorno, no necesariamente
homogéneas, siendo ![]() .
.
Si, por ejemplo, las condiciones son de tipo Dirichlet, entonces
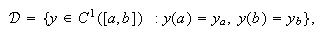 con
con ![]() e
e ![]() reales. Por
lo tanto, para poder considerar las funciones coordenadas (tanto polinómicas
como trigonométricas) que se han indicado anteriormente, será necesario
homogeneizar previamente dichas condiciones de contorno. Esto equivale a
realizar el cambio de variable dependien-te
reales. Por
lo tanto, para poder considerar las funciones coordenadas (tanto polinómicas
como trigonométricas) que se han indicado anteriormente, será necesario
homogeneizar previamente dichas condiciones de contorno. Esto equivale a
realizar el cambio de variable dependien-te
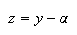 con
con 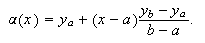 Se cumple, pues, que
Se cumple, pues, que
![]() .
.
Es fácil determinar, por procedimientos similares, los cambios de variable dependiente necesarios para homogeneizar los otros tipos de condiciones de frontera considerados.
Homogeneizadas las condiciones de contorno, para cada ![]() se podrá
definir la función
se podrá
definir la función ![]() dada por
dada por
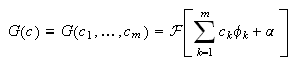 que equivale a considerar el
funcional
que equivale a considerar el
funcional ![]() restringido al espacio de funciones finito-dimensional
restringido al espacio de funciones finito-dimensional 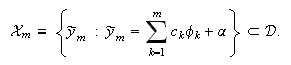
La idea pues es que, optimizando esta función de varias variables, es decir buscando dónde alcanza sus valores máximos o mínimos, estaremos de hecho calculando de forma aproximada los valores extremos que alcanza el funcional de partida. Por ello, para aproximar las extremales de aquél, te-ne-mos que empezar buscando cuáles son los puntos críticos de esta función de varias variables.
Hay que resolver, por tanto, el sistema de ecuaciones
 que, en general, puede ser no
lineal, a no ser que la función
que, en general, puede ser no
lineal, a no ser que la función ![]() sea cuadrática en todas y
cada una de sus componentes.
sea cuadrática en todas y
cada una de sus componentes.
Así pues, la solución del sistema anterior, que podemos denotar ![]() , proporcionará la función
, proporcionará la función
![]()
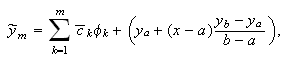 que
será una aproximación de las verdaderas extremales
que
será una aproximación de las verdaderas extremales ![]() del
funcional
del
funcional ![]() en el
dominio de funciones
en el
dominio de funciones ![]() . También es lógico
esperar que aquellas extremales que proporcionen máximos o mínimos del funcional
se correspondan también con máximos y mínimos, respectivamente, de la función
considerada.
. También es lógico
esperar que aquellas extremales que proporcionen máximos o mínimos del funcional
se correspondan también con máximos y mínimos, respectivamente, de la función
considerada.
Además, si el funcional estuviese acotado inferiormente y, por ejemplo, ![]() , notaremos
, notaremos 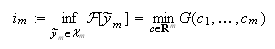 y
obtenemos una sucesión decreciente de cotas superiores de dicho ínfimo,
y
obtenemos una sucesión decreciente de cotas superiores de dicho ínfimo, ![]() ,
,![]() que convergerá
en la mayor parte de los casos que consideraremos en la práctica.
que convergerá
en la mayor parte de los casos que consideraremos en la práctica.
En general, cuando se puede encontrar una sucesión ![]() tal que
tal que ![]() , se dice que
ésta es una sucesión minimizante.
, se dice que
ésta es una sucesión minimizante.
No obstante, aunque es relativamente fácil encontrar sucesiones minimizantes
cuando el funcional está acotado inferiormente, el mayor problema queda sin
resolver. Esto es debido a que estas sucesiones no tienen por qué ser
convergentes, e incluso en el caso de converger hacia una ![]() , tampoco se tiene
asegurado que
, tampoco se tiene
asegurado que ![]() .
.
Uno de los resultados teóricos más generales aplicable en este tipo de situaciones se presenta para un espacio de Hilbert separable, eligiendo un conjunto de funciones coordenadas satisfaciendo las propiedades propiedad1- propiedad3, cuando el funcional es coercivo y débilmente semicontinuo (consultar, por ejemplo, Blan-Bru). Para ver alguna de las primeras aplicaciones en mecánica se puede consultar también los artículos clásicos Duncan.
Vamos a aplicar el método de Ritz para resolver problemas de contorno asociados a la ecuación lineal
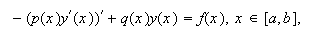 donde
donde ![]() y
y ![]()
Sabemos que este problema de contorno en forma autoadjunta proviene de la búsqueda de las extremales del funcional
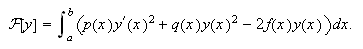
Para ver esto, bastará con escribir la correspondiente ecuación de Euler-Poisson, que es una condición necesaria de
extremo de clase ![]() para el funcional (funcpcautoadj), con
para el funcional (funcpcautoadj), con 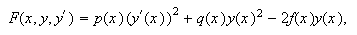 que adopta la forma
que adopta la forma 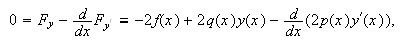 y
que no es más que la indicada en (pobcautoadj), salvo el factor común
y
que no es más que la indicada en (pobcautoadj), salvo el factor común ![]() .
.
Supondremos que ![]() es positiva en
es positiva en ![]() . Si también se verifica que
. Si también se verifica que ![]() es no negativa, entonces
se puede ver, gracias a la convexidad del funcional, que
es no negativa, entonces
se puede ver, gracias a la convexidad del funcional, que ![]() alcanza un único mínimo absoluto en el correspondiente espacio de funciones
(cdDirichlet), con condiciones de contorno de
tipo Dirichlet.
alcanza un único mínimo absoluto en el correspondiente espacio de funciones
(cdDirichlet), con condiciones de contorno de
tipo Dirichlet.
Si suponemos que ya se han homogeneizado las condiciones de frontera de tipo
Dirichlet, mediante el cambio indicado en (cambiocchDirichlet), entonces la
aproximación ![]() -ésima
se buscará de la forma
-ésima
se buscará de la forma ![]() .
.
Ahora bien, 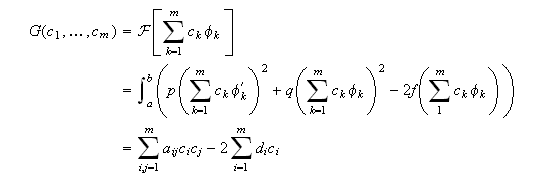 siendo
siendo 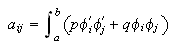 y
y 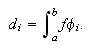 Evidentemente,
Evidentemente, ![]() para cualesquiera
para cualesquiera ![]() y
y ![]() .
.
Así, ![]() es un
polinomio de segundo grado en
es un
polinomio de segundo grado en ![]() variables, y el sistema
que se obtiene al buscar los puntos críticos es lineal (salvo un factor
constante
variables, y el sistema
que se obtiene al buscar los puntos críticos es lineal (salvo un factor
constante ![]() ).
Concretamente,
).
Concretamente, ![]() es un punto crítico de
es un punto crítico de
![]() si y sólo si
si y sólo si
![]() , con
, con 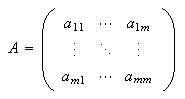 y
y
![]() .
.
Se demuestra que, al menos en el caso indicado
anteriormente, con ![]() y
y ![]() ,
, ![]() , este sistema
lineal tiene solución y ésta es única. De hecho, también se comprueba
fácilmente que se trata de una matriz simétrica y definida positiva, con las
hipótesis hechas sobre las funciones
, este sistema
lineal tiene solución y ésta es única. De hecho, también se comprueba
fácilmente que se trata de una matriz simétrica y definida positiva, con las
hipótesis hechas sobre las funciones ![]()
![]() y
y ![]() .
.
Demostración.- La simetría de la matriz ![]() se deduce de la
definición de sus coeficientes, que aparece en (defsistlineal1). Utilizando la
interpretación que tiene el hecho de que suponiendo un problema homogéneo, con
una función
se deduce de la
definición de sus coeficientes, que aparece en (defsistlineal1). Utilizando la
interpretación que tiene el hecho de que suponiendo un problema homogéneo, con
una función ![]() en el segundo miembro de (pobcautoadj), entonces tendríamos que
en el segundo miembro de (pobcautoadj), entonces tendríamos que 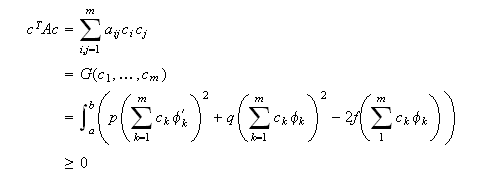 De
De
![]() deduciríamos que
deduciríamos que ![]() . Integrando,
encontraríamos que
. Integrando,
encontraríamos que ![]() . Como el problema del
que partimos tiene condiciones homogéneas, entonces la única posibilidad es que
. Como el problema del
que partimos tiene condiciones homogéneas, entonces la única posibilidad es que
![]() . De la
independencia lineal de las funciones coordenadas se deduce que
. De la
independencia lineal de las funciones coordenadas se deduce que ![]() . Se concluye, pues, que
. Se concluye, pues, que
![]() es definida
positiva y el correspondiente sistema lineal homogéneo
es definida
positiva y el correspondiente sistema lineal homogéneo ![]() tendría como
única solución la trivial y cualquier otro (para una función
tendría como
única solución la trivial y cualquier otro (para una función ![]() )
sería compatible determinado, con una única solución por lo tanto.
)
sería compatible determinado, con una única solución por lo tanto. ![]()
Como indicábamos anteriormente, el método de Galerkin nos permitirá aproximar no sólo problemas autoadjuntos sino también problemas que no estén relacionados directamente con la optimización de un funcional. Esto se debe a que este método se basa en la denominada formulación variacional del correspondiente problema diferencial, como veremos más adelante.
Esta formulación variacional será totalmente equivalente al problema de partida para soluciones suficientemente regulares, ya que bastará con realizar las correspondientes integraciones por partes en el sentido inverso y aplicar el conocido lema fundamental del Cálculo de Variaciones para obtener la ecuación de partida.
Sin embargo, para funciones que no sean suficientemente diferenciables eesto no será posible; pero esta formulación variacional seguirá teniendo completo sentido ya que en su planteamiento apenas se requieren condiciones de regularidad de la solución, salvo que existan y estén bien definidas las integrales involucradas. Es por ello que muchas veces también se suele llamar formulación débil a esta formulación variacional, ya que a partir de ella se pueden debilitar considerablemente las condiciones de regularidad de la solución. Como veremos, ésta será la vía para ampliar el concepto de solución de una ecuación diferencial para admitir soluciones generalizadas (no regulares) también llamadas soluciones débiles.
En particular, ésta será también la vía ideal para encontrar soluciones aproximadas que sean polinómicas a trozos y con una regularidad a menudo bastante inferior a la de la solución exacta del problema de partida. Así pues, esta formulación variacional o débil es también la base para aplicar el conocido como método de los elementos finitos, que veremos con más detenimiento en un capítulo posterior.
De esta manera, el método de Galerkin resulta ser también un caso particular de aplicación en el correspondiente espacio finito-dimensional formado por las llamadas funciones test de una técnica denominada de los residuos ponderados, en la que se intenta minimizar el denominado residuo para la solución aproximada, que para la solución exacta en el espacio total sería nulo.
Otra interpretación de este hecho también sería el hecho de encontrar la mejor aproximación de la solución exacta en un subespacio de dimensión finita, estando caracterizada esta mejor aproximación por el hecho de que la diferencia entre la solución exacta y la aproximada será ortogonal (respecto a cierto producto escalar adecuado) a todos los elementos del subespacio y, en particular, a todos los de la base del subespacio.
Consideramos, por ejemplo, el problema de contorno con condiciones de tipo Dirichlet
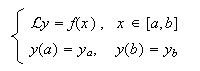 siendo
siendo ![]() una función real de
variable real suficientemente deri-va-ble y
una función real de
variable real suficientemente deri-va-ble y ![]() un
operador diferencial lineal de segundo orden, dado en forma autoadjunta, o no
autoadjunta, respectivamente:
un
operador diferencial lineal de segundo orden, dado en forma autoadjunta, o no
autoadjunta, respectivamente: 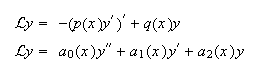
Suponemos en todo caso que las funciones que definen estos operadores cumplen
las propiedades usuales en cuanto a regularidad y signo: ![]() y
y ![]() , con
, con ![]() ,
, ![]() , en el caso autoadjunto,
y
, en el caso autoadjunto,
y ![]() , en el caso no
autoadjunto. De hecho, se puede ver que cuando
, en el caso no
autoadjunto. De hecho, se puede ver que cuando ![]() no se anula
en
no se anula
en ![]() entonces el problema puede escribirse en forma autoadjunta,
poniendo
entonces el problema puede escribirse en forma autoadjunta,
poniendo 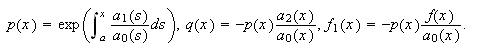
Un problema diferencial, como los enunciados anteriormente, se puede plan-tear de una forma equivalente de la siguiente manera:
primero se multiplican ambos miembros de la ecuación por una función test
que satisface ciertas condiciones, por ejemplo, ![]()
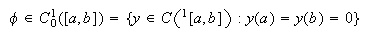
y se realiza la integración en el intervalo ![]() en ambos miembros:
en ambos miembros: 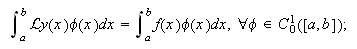
posteriormente se puede hacer las integraciones por partes que resulte conveniente y debilitar así las condiciones de regularidad exigidas a la posible solución, obteniéndose de este modo las correspondientes formulaciones variacional y débil del problema de partida.
Por conveniencia del lector incluimos a continuación la demostración del lema fundamental del Cálculo Variacional y la de la enunciada equivalencia entre el problema de contorno de partida y sus correspondiente formulación variacional, para soluciones suficientemente regulares.
Para ello necesitamos introducir los siguientes espacios de funciones (de
manera recursiva): 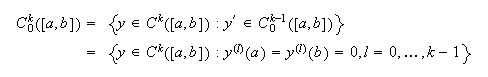
Si la función continua ![]() cumple que
cumple que
![]() para toda
función
para toda
función ![]() , con
, con
![]() ,
entonces
,
entonces ![]() .
.
Demostración.- La demostración de este lema fundamental
no puede ser más simple e inmediata; la haremos por reducción al absurdo. Si
![]() para algún
para algún ![]() , el teorema de
conservación del signo garantiza la existencia de un intervalo
, el teorema de
conservación del signo garantiza la existencia de un intervalo ![]() en el que
en el que ![]() tiene el
signo de
tiene el
signo de ![]() .
Podemos encontrar una función
.
Podemos encontrar una función ![]() tal que
tal que ![]() ,
, ![]() , y sin embargo
, y sin embargo ![]() ,
, ![]() . Una posible elección es
. Una posible elección es
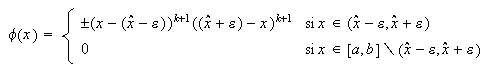 Observemos que
Observemos que 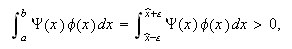 lo
que contradice la hipótesis del lema.
lo
que contradice la hipótesis del lema. ![]()
Vemos ahora cómo podemos replantear la relación (formintegral): restando ambos miembros, para toda
función ![]() se
verifica que
se
verifica que
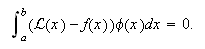 Por el lema fundamental del
Cálculo de Variaciones,con
Por el lema fundamental del
Cálculo de Variaciones,con ![]() , obtenemos la ecuación
del problema de partida (Pbmacontorno) para
soluciones suficientemente regulares (como para que
, obtenemos la ecuación
del problema de partida (Pbmacontorno) para
soluciones suficientemente regulares (como para que ![]() sea continua).
sea continua).
Cuando las condiciones de contorno no son homogéneas, lo mejor es
homogeneizarlas y plantear un problema equivalente 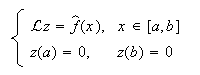 con
con
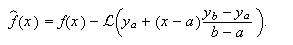
Por ejemplo, en el caso autoadjunto, tendremos
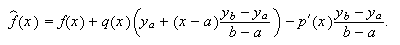
Podremos considerar entonces ![]() , de manera que cualquier
combinación lineal de éstas seguirá cumpliendo las condiciones de Dirichlet
homogéneas.
, de manera que cualquier
combinación lineal de éstas seguirá cumpliendo las condiciones de Dirichlet
homogéneas.
El método de Galerkin consiste en buscar soluciones aproximadas, en el
espacio ![]() , del problema equivalente (pbmahomegeneizado), pero considerado en su
formulación variacional (formintegral). Para
ello buscamos
, del problema equivalente (pbmahomegeneizado), pero considerado en su
formulación variacional (formintegral). Para
ello buscamos ![]() tal que
tal que 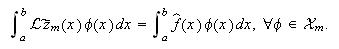 Así
pues, bastará con que se verifique para el sistema de generadores del espacio
Así
pues, bastará con que se verifique para el sistema de generadores del espacio
![]() ,
es decir, para las funciones
,
es decir, para las funciones ![]() ,
,![]()
Ahora bien, como ![]() es una base del espacio
es una base del espacio
![]() ,
entonces
,
entonces ![]() quedará completamente determinada cuando se conozca el valor de cada una de las
componentes
quedará completamente determinada cuando se conozca el valor de cada una de las
componentes ![]() ,
,
![]() .
.
Esto plantea la re-so-lución del sistema lineal
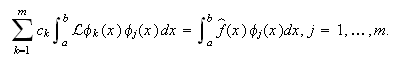 Notando
Notando ![]()
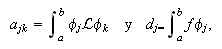 obtenemos su forma
matricial habitual:
obtenemos su forma
matricial habitual: 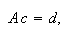 donde
donde 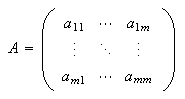 y
y ![]() .
.
Se comprueba que, en general, para un problema no autoadjunto esta matriz puede no ser simétrica; sin embargo, para un problema de contorno autoadjunto, bastará tener en cuenta que
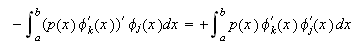 para obtener exactamente la misma
expresión para los elementos de la matriz que la que se obtuvo al emplear la
idea de Ritz. Vemos pues, que para el caso de problemas autoadjuntos, ambos
métodos son equivalentes; sin embargo el método de Galerkin es aplicable también
al caso no autoadjunto.
para obtener exactamente la misma
expresión para los elementos de la matriz que la que se obtuvo al emplear la
idea de Ritz. Vemos pues, que para el caso de problemas autoadjuntos, ambos
métodos son equivalentes; sin embargo el método de Galerkin es aplicable también
al caso no autoadjunto.
P. Blanchard, E. Brüning, ``Variational Methods in Mathematical Physics: A Unified Approach''. Springer-Verlag (Text and Monographs in Physics).
W.J. Duncan en Gr. Brit. Aeronaut. Res. Comm. Reports and Mem. num. 1798 y 1848.
V. Ramírez, P. González, M. Pasadas, D. Barrera, "MATEMÁTICAS con Mathematica: Cálculo Numérico", Proyecto Sur de Ediciones (1997).