All the surfaces below are obtained by solving a Plateau problem for a non compact polygonal curve, and extending this solution by successive Schwarz reflections.




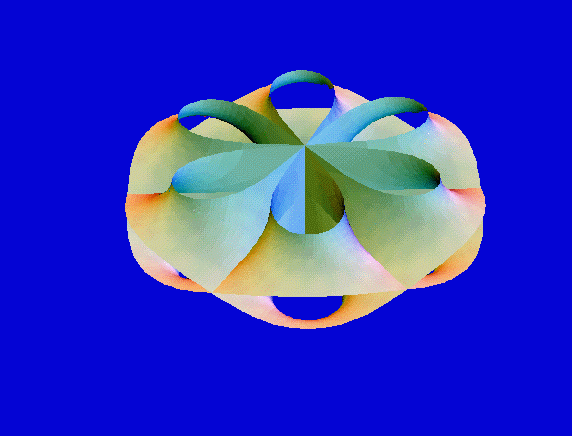



|
All the surfaces below are obtained by solving a Plateau problem for a non compact polygonal curve, and extending this solution by successive Schwarz reflections.
|
||
 |
 |
 |
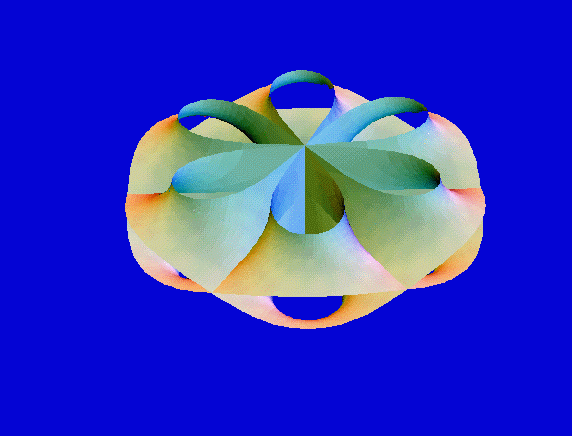 |
||
 |
 |
 |
| Minimal
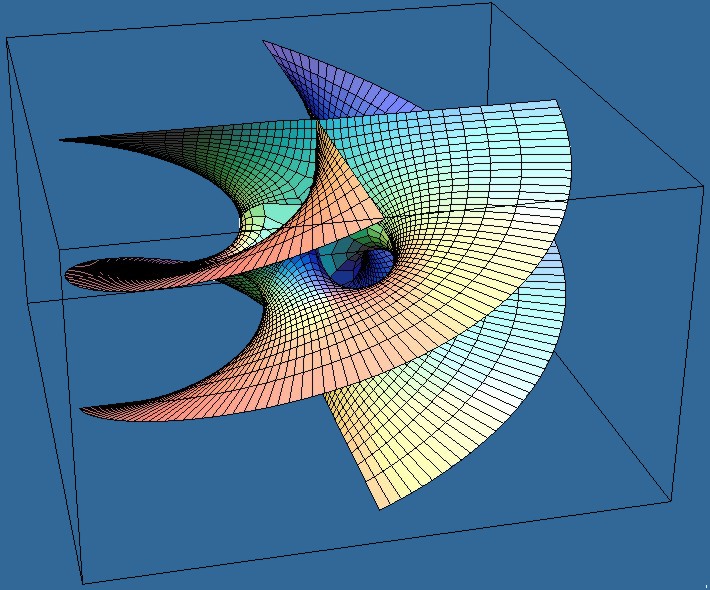
surfaces with helicoidal ends. By the deforming the above surfaces, we get minimal surfaces with helicoidal ends. The example on the right corresponds to a non-orientable minimal helicoid due to L. Ferrer and F. Martín. |
 |
Mathematica 2.2 for Solaris.