EJERCICIOS DE FUERZA Y PRESIÓN

PRESIÓN

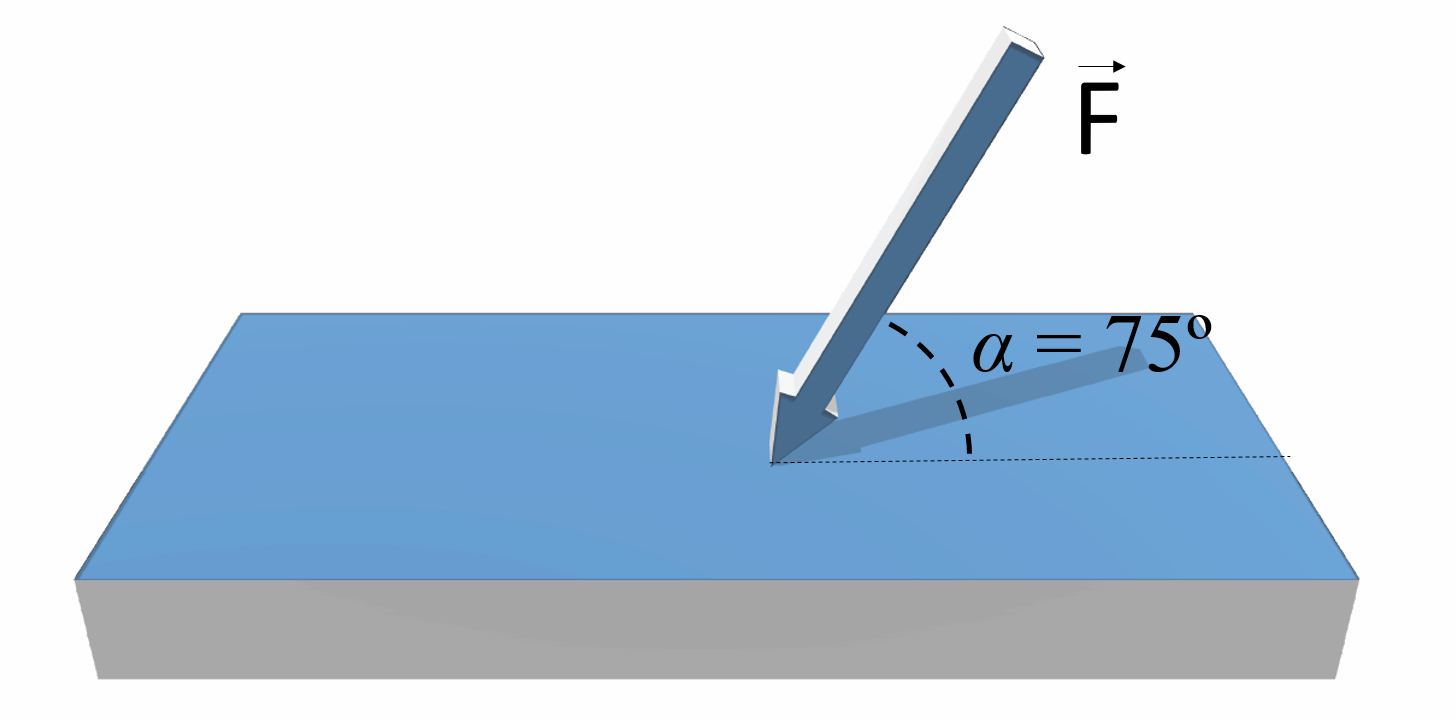
1. En la siguiente figura, la fuerza es $F=2\mbox{ N}$. Calcular la presión ejercida sobre la superficie de 2 m$^2$ de área.
   

   

   Solución

   SOLUCIÓN:
   Primero hay que calcular la componente de la fuerza normal a la superficie, es decir: $$F_n=F\sin\left(\alpha\right)=2\sin\left(25^\circ\right)=0.845\mbox{ N}$$ Y la presión será:
   $$P=\frac{F_n}{S}=\frac{0.845\mbox{ N}}{2\mbox{ m}^2}$$

   $P=0.42\mbox{ Pa}$

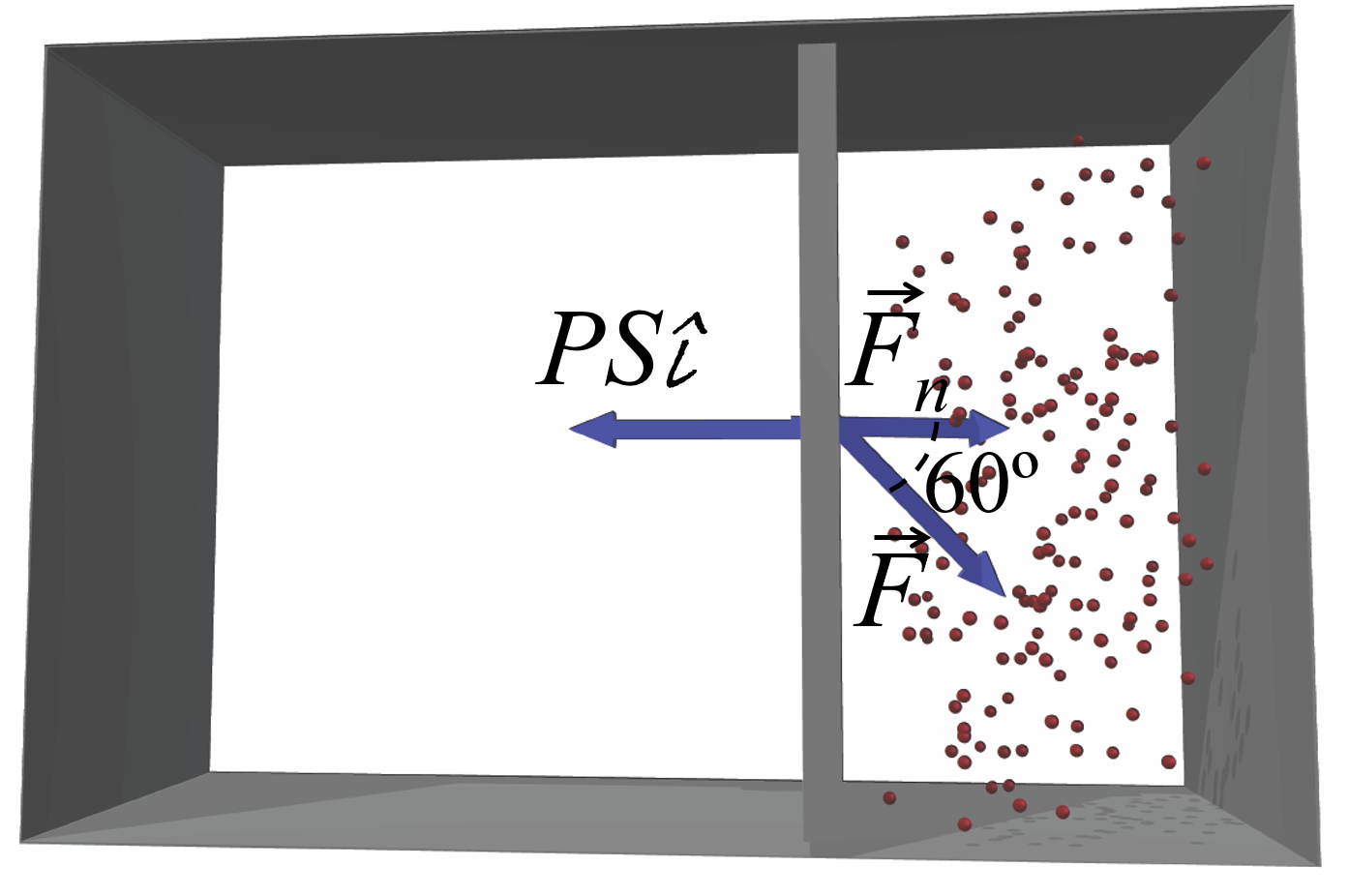
2. En la siguiente figura, el recipiente contiene un gas a presión $P=2\mbox{ atm}$. Calcular la fuerza $F$ necesaria para que el émbolo de 2 m$^2$ no se mueva.
   

   

   Solución

   SOLUCIÓN:
   En la siguiente figura se hace un esquema de fuerzas.

   

   El gas encerrado en la cámara ejerce una fuerza de presión sobre la plataforma perpendicular hacia ella e igual a $PS(-\hat{\imath})$. Para que esté en equilibrio, la componente normal de la fuerza aplicada debe compensar esta fuerza: $$\vec{F}_n+PS(-\hat{\imath})=0$$ $$F\cos\left(60^\circ\right)-PS=0$$ Por lo tanto, $$F=\frac{PS}{\cos\left(60^\circ\right)}$$ Antes de operar, pasamos todas las magnitudes al mismo sistema de unidades: $$P=2\mbox{ atm}=2\mbox{ atm}\cdot 101300\frac{\mbox{ Pa}}{\mbox{ atm}}=202600\mbox{ Pa}$$ $$F=\frac{202600\mbox{ Pa}\cdot 2\mbox{ m}^2}{\cos\left(60^\circ\right)}=810.4\mbox{ kN}$$

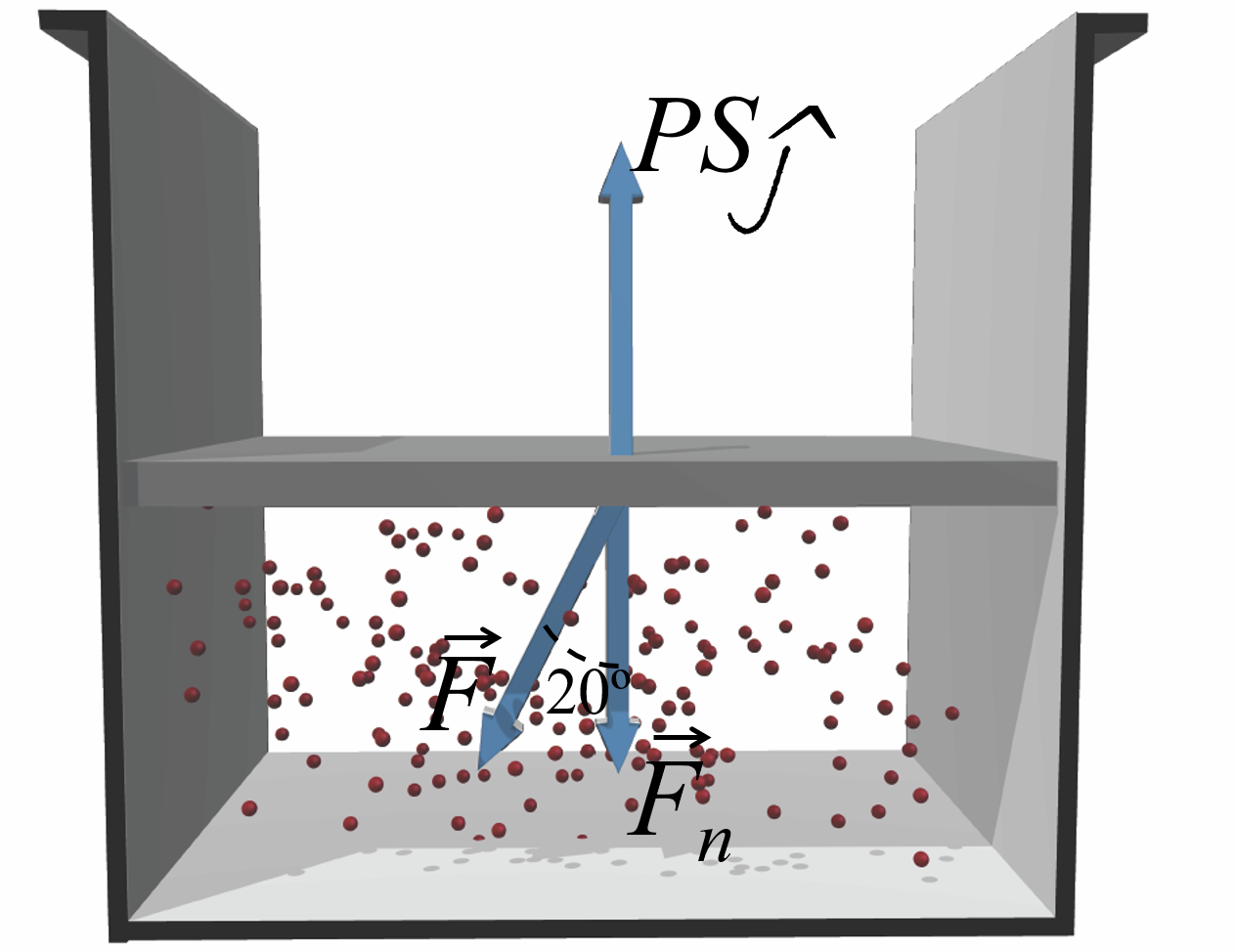
3. En la siguiente figura, el recipiente contiene un gas a presión $P=2300\mbox{ dinas/cm}^2$. Calcular la fuerza $F$ en N necesaria para que la plataforma de 2 m$^2$ no se mueva.
   

   

   Solución

   SOLUCIÓN:
   Al igual que antes, las fuerzas que actúan sobre la plataforma son, la fuerza de presión hacia arriba y la fuerza aplicada.

   

   Para que esté en equilibrio, la componente normal de la fuerza aplicada debe compensar la fuerza de presión: $$\vec{F}_n+PS(\hat{\jmath})=0$$ $$-F\cos\left(20^\circ\right)+PS=0$$ Por lo tanto, $$F=\frac{PS}{\cos\left(20^\circ\right)}=48.95\mbox{ kN}$$

   Antes de operar, pasamos todas las magnitudes al mismo sistema de unidades: $$P=2300\mbox{ dinas/cm}^2=2300\mbox{ dinas/cm}^2\cdot\frac{1}{10\frac{\mbox{ dinas/cm}^2}{\mbox{ Pa}}}=230\mbox{ Pa}$$ $$F=\frac{230\mbox{ Pa}\cdot 2\mbox{ m}^2}{\cos\left(20^\circ\right)}=490\mbox{ N}$$

4. ¿En la siguiente figura, ¿en qué dirección sale el fluido de la jeringa?
   

   

   Solución

   SOLUCIÓN:
   El fluidos sale por los agujeros empujado por la fuerza de la presión. Esta es perpendicular al agujero y por tanto, independientemente de la dirección del agujero, el fluido sale perpendicular a él.

PRESIÓN HIDROSTÁTICA

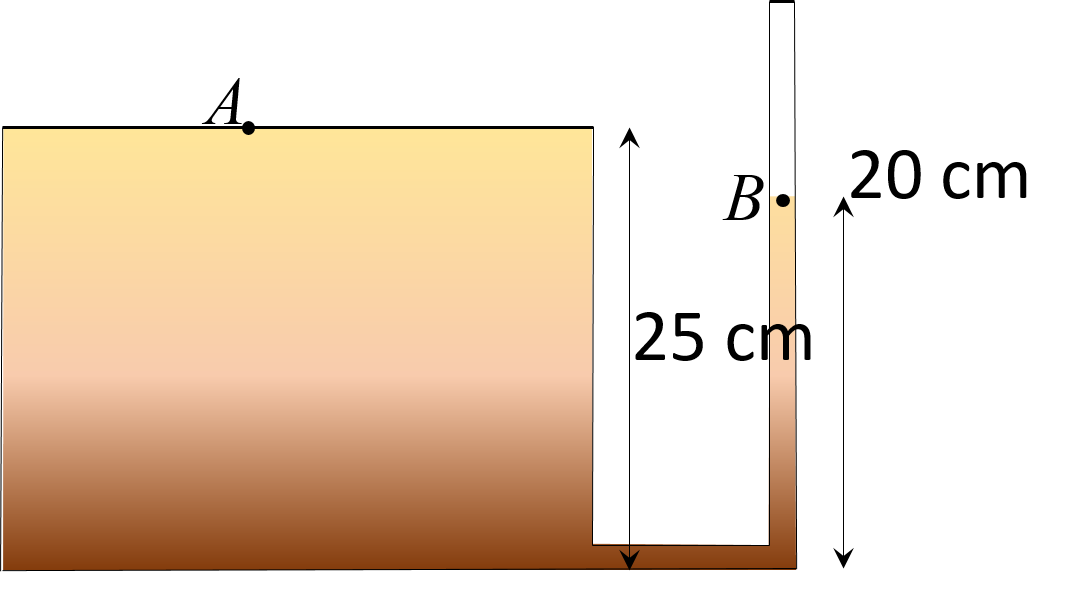
5. El tanque de la figura está lleno de agua y lleva adosado un tubo por el que asciende el fluido. La presión en B es 1500 Pa. a) Calcular la presión en el fondo. b) Calcular la presión en A.
   

   

   Solución

   SOLUCIÓN:
   

   1. Por la ecuación de la hidrostática: $$P_{fondo}=P_B+dgh$$ siendo $h$ la profundidad desde el punto B. Por lo tanto: $$P=1500\mbox{ Pa}+1000\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot 0.25\mbox{ m}=3950\mbox{ Pa}$$

   2. De nuevo aplicamos la ecuación de la hidrostática: $$P_A=P_B+dgh$$ siendo $h$ la diferencia de altura entre ambos puntos.
      ¡OJO! Fíjese en el orden. Siempre h es la profundidad desde el punto B, es decir, en esta ecuación, se calcula la presión de un punto B que está más profundo que otro punto A.
      Por lo tanto: $$P=1500\mbox{ Pa}+1000\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot (0.25-0.2)\mbox{ m}=1990\mbox{ Pa}$$

6. En el tanque de la figura, lleno de agua, la presión en el punto B es 1500 Pa. Calcular la presión en A.
   

   

   Solución

   SOLUCIÓN:
   Por la ecuación de la hidrostática: $$P_B=P_A+dgh$$ Fíjese que ahora B está más profundo. Como queremos calcular la presión en A: $$P_A=P_B-dgh$$ Por lo tanto: $$P=1500\mbox{ Pa}-1000\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot (0.25-0.2)\mbox{ m}=1010\mbox{ Pa}$$

7. El tubo de la figura está lleno de un aceite de densidad 0.65 g/ml. La presión en B es 28000 Pa. Calcular la presión en A.
   

   

   Solución

   SOLUCIÓN:
   Por la ecuación de la hidrostática: $$P_A=P_B+dgh$$ Fíjese que hemos escogido un punto A en el borde del tubo. Sin embargo, aunque no tenga fluido justo encima, tiene fluido en los alrededores y por tanto ejerce presión sobre A. Para calcularlo, de nuevo da igual la posición, sólo hay que tener en cuenta la diferencia de altura. $$P=28000\mbox{ Pa}+650\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot 0.1\mbox{ m}=28637\mbox{ Pa}$$

8. El tubo de la figura está lleno de un aceite de densidad 0.65 g/ml. La presión en A es 1 atm. Calcular la presión en B.
   

   

   Solución

   SOLUCIÓN:
   Por la ecuación de la hidrostática: $$P_A=P_B+dgh$$ Fíjese que da igual la forma del tubo y la posición dentro de él. Sólo hay que tener en cuenta la diferencia de altura. Como queremos calcular la presión en B: $$P_B=P_A-dgh$$ Por lo tanto: $$P=101300\mbox{ Pa}-650\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot (0.2-0.05)\mbox{ m}=100345\mbox{ Pa}$$