En la siguiente figura, la presión atmosférica es \(P_{atm}\)=0.8 atm. Calcule la altura que ascenderá el mercurio en un barómetro.
SOLUCIÓN:
En A’: \(P(A')=0.8 \text{ atm}=0.8\cdot 101300 \text{ Pa/atm}=81040 \text{ Pa}\). Como A y A’ están a la misma altura, la presión es la misma. Por otro lado, la presión en B es 0, ya que no hay ningún fluido encima. Por lo tanto: \[P(A')=P_B+dgH=dgH\] Como el fluido es mercurio, \(d=13500 \text{ kg/m}^3\). Despejando \(H\): \[H=\frac{P(A')}{dg}=\frac{81040\mbox{ Pa}}{13600\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2}=0.608\mbox{ m}\] El mercurio asciende 608 mm por la columna.
A partir de la siguiente figura, calcule la presión atmosférica. Exprese el resultado en torr.
SOLUCIÓN:
Dado que me lo piden en torr, por definición, esto es justamente la altura en mm de la columna de mercurio, es decir: \[P_{atm}=810\mbox{ torr}\] Lo podemos comprobar así: hacemos un esquema similar al ejercicio anterior. Entonces: \[P_{atm}=P(A)=P_B+dgH=dgH\] \[P_{atm}=13600\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot 0.81\mbox{ m}=107957\mbox{ Pa}\] Y pasando a torr: \[P_{atm}=107957\mbox{ Pa}\cdot \frac{101300\mbox{ Pa}}{760\mbox{ torr}}=810\mbox{ torr}\]
La presión atmosférica en un punto dado son 980 mbar. Exprese este valor en atm, Pa, torr y dinas/cm\(^2\).
SOLUCIÓN:
1 mbar = 100 Pa, entonces
El tanque de la figura lleva adosado un tubo por el que asciende el fluido. El líquido es agua. a) Calcular la presión en el fondo. b) ¿Cuál será la altura del agua en el tanque?
SOLUCIÓN:
Para ello aplicamos la ecuación de la hidrostática: \[P=P_0+dgh\] siendo \(P_0\) la presión en la superficie libre del tubo. Como el tubo está abierto, \(P_0=P_{atm}=101300 \text{ Pa}\). Por lo tanto: \[P=101300\mbox{ Pa}+1000\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot 1.5\mbox{ m}=116000\mbox{ Pa}\]
Dado que la presión no depende A una misma altura, la presión ha de ser la misma, tanto en el tanque como en el tubo. En particular esto es así en la superficie libre, donde tendremos la presión atmosférica, tanto en el tanque como en el tubo. Por lo que la superficie libre ha de estar en la misma altura: 1.5 m.
¿Y si en vez del tanque tengo un recipiente como el de las siguientes figuras? ¿Cambia la presión?
SOLUCIÓN:
La presión varía sólo con la altura, independientemente de la forma del recipiente. Por tanto, la altura ha de ser siempre la misma.
Ahora el tanque está cerrado. Esto quiere decir que no está en contacto con la atmósfera. En las condiciones del dibujo, calcula la presión en la superficie libre del tanque (punto A).
SOLUCIÓN:
Para encontrar la solución, buscamos un punto donde conozcamos la presión. Como el tubo está abierto, la presión en su parte superior será la presión atmosférica: \[P_0=101300\mbox{ Pa}\]
Y como la presión sólo depende de la diferencia de altura: \[P_A=P_0+dgH=101300\mbox{ Pa}+1000\mbox{ kg/m}^3\cdot 9.8\mbox{ m/s}^2\cdot 1\mbox{ m}=111100\mbox{ Pa}\]
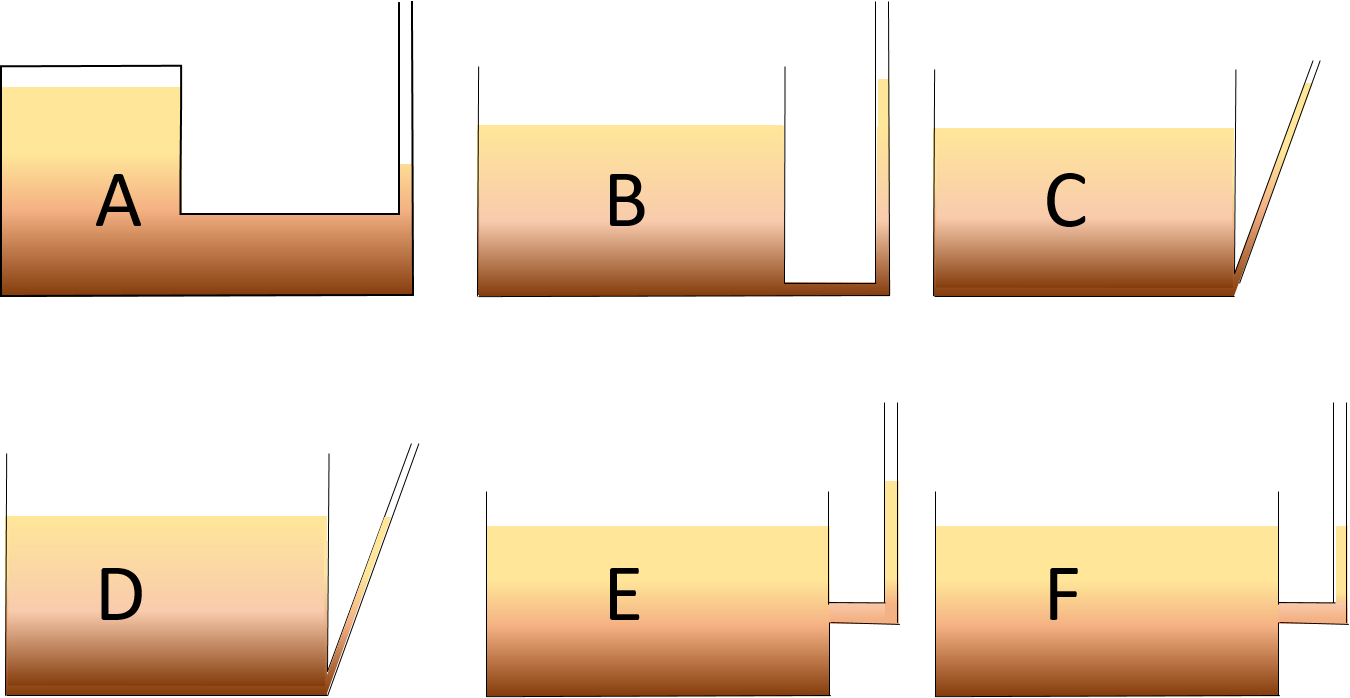
De las siguientes figuras, indica cuáles son imposibles y explica la razón.
SOLUCIÓN:
A: Sí es posible, ya que el tanque está cerrado, la presión en la cámara de aire no tiene por qué ser la misma que la exterior. En particular, en este caso la presión es menor, ya que la superficie está más alta.
B: No es posible. El tanque está abierto y por tanto la presión ha de ser la presión atmosférica. Como la presión sólo depende de la altura, y dado que la presión es la misma en las superficies libres en el tubo y en el tanque, la altura debe ser también la misma.
C: No es posible, por los mismos argumentos que en B. Da igual la forma que tenga el tubo o su anchura.
D: Sí es posible. La presión es igual en ambas superficies libres, tanque y tubo, por lo tanto también su altura. No importa la forma o anchura del tubo.
E: No es posible. Da igual dónde esté conectado el tubo. Siempre que los líquidos en tubo y tanque estén conectados, la presión sólo será función de la profundidad desde la superficie libre.
F: Sí es posible. La superficie libre está a la misma altura, como se corresponde con el hecho de que la presión es la misma.
Volver a la página principal de Física