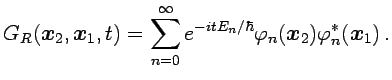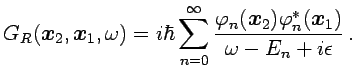
Siguiente: 3.2 Propagador euclídeo. Arriba: 3 Fórmula de Feynman-Kac Anterior: 3 Fórmula de Feynman-Kac

3.1 Propiedades del propagador.

Para un hamiltoniano conservativo el propagardor retardado puede escribirse en la forma

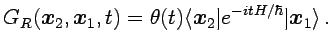$$G_R({{\boldsymbol{x}}}_2,{{\boldsymbol{x}}}_1,t)= \theta(t)\langle{{\boldsymbol{x}}}_2\vert e^{-itH/\hbar}\vert{{\boldsymbol{x}}}_1\rangle \,.$$ (3.1)

Insertando un conjunto de estados propios del hamiltoniano (que suponemos no degenerado por simplicidad)

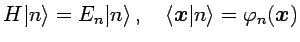$$H\vert n\rangle=E_n\vert n\rangle \,,\quad \langle {{\boldsymbol{x}}}\vert n\rangle=\varphi_n({{\boldsymbol{x}}})$$ (3.2)

se obtiene la representación

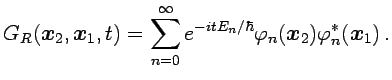$$G_R({{\boldsymbol{x}}}_2,{{\boldsymbol{x}}}_1,t)= \sum_{n=0}^\inf... ... E_n/\hbar}\varphi_n({{\boldsymbol{x}}}_2)\varphi_n^*({{\boldsymbol{x}}}_1) \,.$$ (3.3)

O en representación de frecuencias

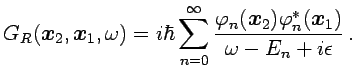$$G_R({{\boldsymbol{x}}}_2,{{\boldsymbol{x}}}_1,\omega)= i\hbar\sum... ...\boldsymbol{x}}}_2)\varphi_n^*({{\boldsymbol{x}}}_1)}{\omega-E_n+i\epsilon} \,.$$ (3.4)

La posición de los polos corresponde al espectro de energía y el residuo proporciona la función de onda.