

Siguiente: 3.4 Fórmula de Feynman-Kac.
Arriba: 3 Fórmula de Feynman-Kac
Anterior: 3.2 Propagador euclídeo.
A nivel microscópico, una partícula browniana en 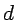 dimensiones
efectúa saltos aleatorios de tamaño
dimensiones
efectúa saltos aleatorios de tamaño 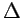 en cualquiera de las
en cualquiera de las 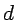 direcciones en tiempos múltiplos de
direcciones en tiempos múltiplos de 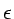 . Macroscópicamente (es
decir, tomando los límites
. Macroscópicamente (es
decir, tomando los límites 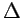 y
y
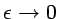 ) la
correspondiente distribución de probabilidad
) la
correspondiente distribución de probabilidad
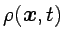 obedece
una ecuación de difusión típica
obedece
una ecuación de difusión típica
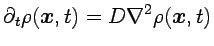 |
(3.7) |
siendo 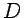 el denominado coeficiente de difusión,
el denominado coeficiente de difusión,
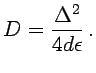 |
(3.8) |
Dado que esta ecuación coincide con la de una partícula libre en
tiempo imaginario
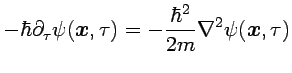 |
(3.9) |
se deduce que la partícula cuántica sigue un movimiento browniano
con coeficiente de difusión
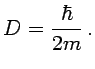 |
(3.10) |
Asimismo, la distribución de probabilidad browniana (de una
partícula inicialmente en
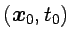 ) puede expresarse mediante
una integral de caminos
) puede expresarse mediante
una integral de caminos
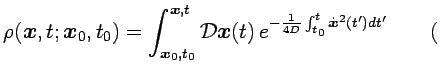 Kac Kac |
(3.11) |
El integrando en esta expresión es la denominada medida de
Wiener. De acuerdo con esta medida, los caminos brownianos son
continuos con probabilidad uno y no diferenciables en ningún punto
también con probabilidad uno.


Siguiente: 3.4 Fórmula de Feynman-Kac.
Arriba: 3 Fórmula de Feynman-Kac
Anterior: 3.2 Propagador euclídeo.
Salcedo
2005-04-27
![]() dimensiones
efectúa saltos aleatorios de tamaño
dimensiones
efectúa saltos aleatorios de tamaño ![]() en cualquiera de las
en cualquiera de las ![]() direcciones en tiempos múltiplos de
direcciones en tiempos múltiplos de ![]() . Macroscópicamente (es
decir, tomando los límites
. Macroscópicamente (es
decir, tomando los límites ![]() y
y
![]() ) la
correspondiente distribución de probabilidad
) la
correspondiente distribución de probabilidad
![]() obedece
una ecuación de difusión típica
obedece
una ecuación de difusión típica
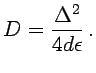
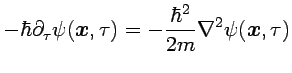
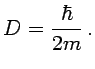
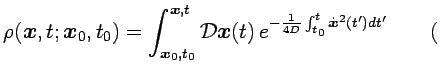 Kac
Kac