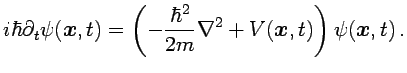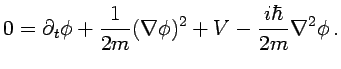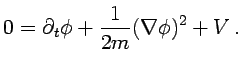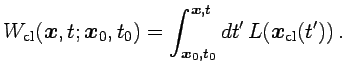

Siguiente: 1.2 Operador de evolución
Arriba: 1 Integral de caminos.
Anterior: 1 Integral de caminos.
Partimos de la ecuación de Schrödinger para una partícula de masa
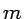 en un potencial
en un potencial 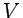
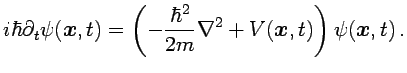 |
(1.1) |
Con el fin de estudiar el límite clásico hacemos el cambio de
variable no lineal
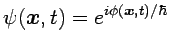 |
(1.2) |
que da lugar a la ecuación equivalente
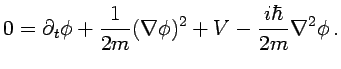 |
(1.3) |
Tomando ahora el límite clásico formal
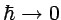 se obtiene la ecuación de Hamilton-Jacobi de la mecánica hamiltoniana
se obtiene la ecuación de Hamilton-Jacobi de la mecánica hamiltoniana
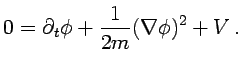 |
(1.4) |
Como es sabido esta ecuación admite como solución la llamada función principal de Hamilton
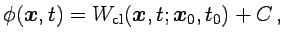 |
(1.5) |
donde 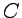 es una constante arbitraria (respecto de
es una constante arbitraria (respecto de
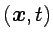 ) y
) y
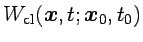 es la acción calculada sobre la
trayectoria solución de las ecuaciones de movimiento con la
condiciones de contorno
es la acción calculada sobre la
trayectoria solución de las ecuaciones de movimiento con la
condiciones de contorno
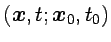 , denominada solución
clásica,
, denominada solución
clásica,
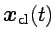 ,
,
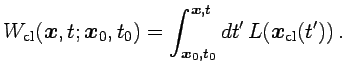 |
(1.6) |
Esto nos indica que, en el límite semiclásico extremo, es válida la
aproximación
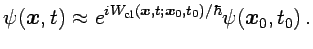 |
(1.7) |


Siguiente: 1.2 Operador de evolución
Arriba: 1 Integral de caminos.
Anterior: 1 Integral de caminos.
Salcedo
2005-04-27
![]() en un potencial
en un potencial ![]()