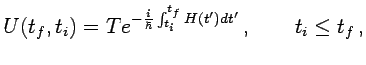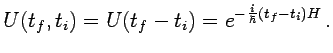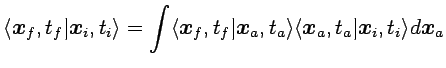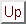

Siguiente: 1.3 Fórmula de Feynman.
Arriba: 1 Integral de caminos.
Anterior: 1.1 Aproximación semiclásica. Ecuación
El análisis de Feynman deriva una versión exacta de la fórmula
(1.7). Para ello se introduce el propagador
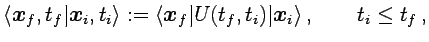 |
(1.8) |
donde 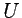 denota el operador de evolución
denota el operador de evolución
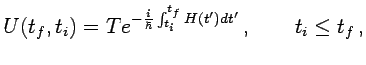 |
(1.9) |
que para hamiltonianos 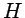 conservativos se simplifica a
conservativos se simplifica a
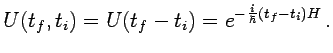 |
(1.10) |
El propagador satisface la propiedad básica
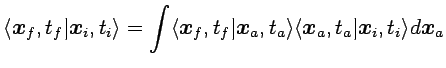 |
(1.11) |
donde 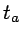 es un tiempo intermedio arbitrario. Esta propiedad
indica que la partícula en
es un tiempo intermedio arbitrario. Esta propiedad
indica que la partícula en
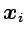 en tiempo
en tiempo 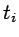 puede llegar a
puede llegar a
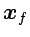 en tiempo
en tiempo 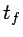 pasando por cualquiera de los puntos
pasando por cualquiera de los puntos
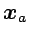 en el tiempo intermedio
en el tiempo intermedio 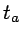 , con mayor o menor amplitud de
probabilidad, dependiendo del propagador.
, con mayor o menor amplitud de
probabilidad, dependiendo del propagador.
Salcedo
2005-04-27