

Siguiente: 2.2 Acciones cuadráticas.
Arriba: 2 Integral de caminos
Anterior: 2 Integral de caminos
El lagrangiano de una partícula no relativista en un campo electromagnético
es
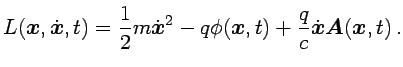 |
(2.1) |
Como es sabido, bajo una transformación de gauge de los potenciales
escalar y vector
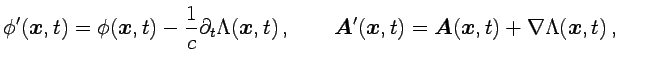 |
(2.2) |
el lagrangiano se transforma como
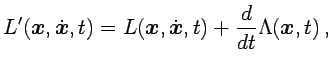 |
(2.3) |
y las ecuaciones de movimiento quedan invariantes (actúa la fuerza de Lorentz
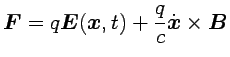 |
(2.4) |
que es invariante gauge).
En el caso cuántico se obtiene la misma invariancia teniendo en cuenta
que la función de onda se transforma según
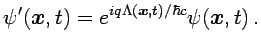 |
(2.5) |
Este resultado corresponde a una transformación unitaria en la
formulación canónica y se obtiene en forma muy directa en la
formulación de Feynman. En efecto, el propagador en el nuevo gauge es
![$\displaystyle \langle {{\boldsymbol{x}}}_f,t_f\vert{{\boldsymbol{x}}}_i,t_i\ran...
...\boldsymbol{x}}}(t) \, e^{\frac{i}{\hbar}W^\prime[{{{\boldsymbol{x}}}}(t)]} \,,$](img58.gif) |
(2.6) |
pero, usando (2.3),
![$\displaystyle W^\prime[{{{\boldsymbol{x}}}}(t)] = W[{{{\boldsymbol{x}}}}(t)] +\...
...bda({{\boldsymbol{x}}}_f,t_f)-\frac{q}{c} \Lambda({{\boldsymbol{x}}}_i,t_i) \,,$](img59.gif) |
(2.7) |
que implica
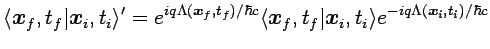 |
(2.8) |
y equivale a (2.5).


Siguiente: 2.2 Acciones cuadráticas.
Arriba: 2 Integral de caminos
Anterior: 2 Integral de caminos
Salcedo
2005-04-27
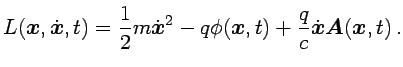
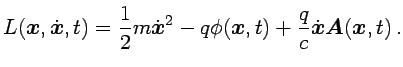
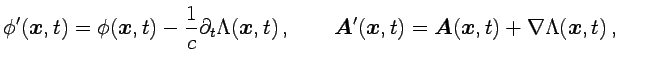
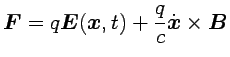
![$\displaystyle \langle {{\boldsymbol{x}}}_f,t_f\vert{{\boldsymbol{x}}}_i,t_i\ran...
...\boldsymbol{x}}}(t) \, e^{\frac{i}{\hbar}W^\prime[{{{\boldsymbol{x}}}}(t)]} \,,$](img58.gif)
![$\displaystyle W^\prime[{{{\boldsymbol{x}}}}(t)] = W[{{{\boldsymbol{x}}}}(t)] +\...
...bda({{\boldsymbol{x}}}_f,t_f)-\frac{q}{c} \Lambda({{\boldsymbol{x}}}_i,t_i) \,,$](img59.gif)