

Siguiente: 3 Fórmula de Feynman-Kac
Arriba: 2 Integral de caminos
Anterior: 2.1 Partícula en un
Cuando la acción es a lo sumo cuadrática en posiciones y velocidades,
la integral funcional es gaussiana y puede hacerse en forma
cerrada. Así para una partícula en una dimensión con lagrangiano
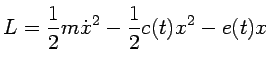 |
(2.9) |
la integral funcional produce
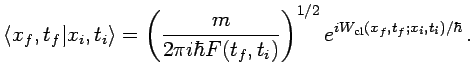 |
(2.10) |
En esta expresión
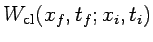 es la acción
evaluada para la trayectoria clásica que une
es la acción
evaluada para la trayectoria clásica que une 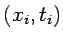 con
con
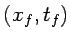 , y la función
, y la función
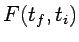 es la solución de la ecuación
es la solución de la ecuación
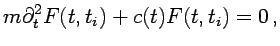 |
(2.11) |
con condiciones de contorno
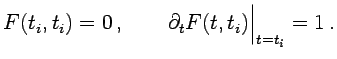 |
(2.12) |
Nótese que la dependencia en las posiciones 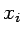 ,
, 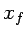 y en el
término lineal del lagrangiano,
y en el
término lineal del lagrangiano, 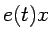 , sólo aparece a través
de la acción clásica. Esta propiedad se extiende a acciones
cuadráticas generales y es inmediata usando integral de caminos.
, sólo aparece a través
de la acción clásica. Esta propiedad se extiende a acciones
cuadráticas generales y es inmediata usando integral de caminos.
Así para la partícula libre se obtiene
![$\displaystyle \langle y,t\vert x,0\rangle = \left(\frac{m}{2\pi i\hbar t}\right)^{1/2} \exp\left[ \frac{im}{2\hbar t}(x-y)^2 \right] \,,$](img72.gif) |
(2.13) |
y para el oscilador armónico de frecuencia angular 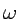
![$\displaystyle \langle y,t\vert x,0\rangle = \left(\frac{m\omega}{2\pi i\hbar \s...
...omega}{2\hbar \sen \omega t}\left((x+y)^2\cos \omega t -2xy \right) \right] \,.$](img74.gif) |
(2.14) |


Siguiente: 3 Fórmula de Feynman-Kac
Arriba: 2 Integral de caminos
Anterior: 2.1 Partícula en un
Salcedo
2005-04-27
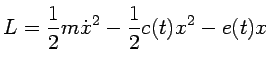
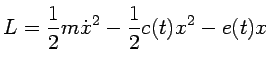
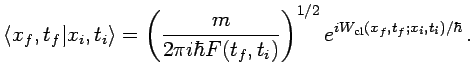
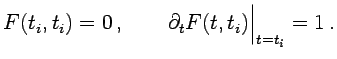
![$\displaystyle \langle y,t\vert x,0\rangle = \left(\frac{m}{2\pi i\hbar t}\right)^{1/2} \exp\left[ \frac{im}{2\hbar t}(x-y)^2 \right] \,,$](img72.gif)
![$\displaystyle \langle y,t\vert x,0\rangle = \left(\frac{m\omega}{2\pi i\hbar \s...
...omega}{2\hbar \sen \omega t}\left((x+y)^2\cos \omega t -2xy \right) \right] \,.$](img74.gif)