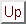

Siguiente: 1.5 Principio de Hamilton.
Arriba: 1 Integral de caminos.
Anterior: 1.3 Fórmula de Feynman.
La expresión (1.13) es formal y tiene sentido riguroso
partiendo del propagador en tiempo imaginario
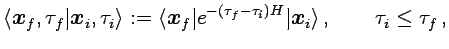 |
(1.15) |
y luego haciedo una extensión analítica desde tiempo imaginario
(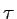 positivo,
positivo, 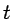 imaginario) a tiempo real (
imaginario) a tiempo real (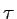 imaginario,
imaginario,
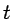 real)
real)
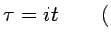 rotación de Wick rotación de Wick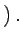 |
(1.16) |
En tiempo imaginario la fórmula de Feynman pasa a
que no contiene contribuciones oscilantes.
Salcedo
2005-04-27
![$\displaystyle \int_{{{{\boldsymbol{x}}}}(\tau_i)={{{\boldsymbol{x}}}_i}}^{{{{\b...
...}(\tau)
\,
\exp \left(-\frac{1}{\hbar}W_E[{{\boldsymbol{x}}}(\tau)] \right) \,,$](img49.gif)